Eine Region ist eine Teilmenge des ![]() .
.
Um ein Venn-Diagramm einwandfrei definieren zu können, ist es zunächst notwendig, einige grundlegende geometrische und topologische Begriffe eindeutig festzulegen.
Ein Punkt heißt innerer Punkt einer Region, wenn es eine Umgebung um diesen Punkt gibt, die vollständig in der Region enthalten ist.
Ein Punkt heißt äußerer Punkt, wenn er innerer Punkt des Komplements der Region ist.
Randpunkt einer Region ist ein Punkt, der weder innerer noch äußerer Punkt ist. Die Menge der Randpunkte bildet den Rand einer Region.
Eine Punktmenge heißt eine Kurve, wenn eine stetige, injektive Abbildung eines Intervalles auf diese Menge existiert.
Eine Region heißt zusammenhängend, wenn zwei beliebige verschiedene Punkte der Region durch eine Kurve verbunden werden können, deren Punkte nur Punkte der Region sind.
Eine Region ist konvex, wenn zwei beliebige verschiedene Punkte der Region durch eine Strecke verbunden werden können, deren Punkte nur innere Punkte der Region sind.
Zur Verdeutlichung einige Beispiele von Kurven und Regionen:
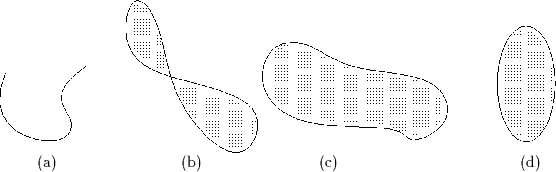
(a) ist eine Kurve, (b) ist eine zusammenhängende Region, wenn der ,,Kreuzungspunkt`` zur Region gehört, sonst ist die Region nicht zusammenhängend, (c) ist eine zusammenhängende Region, (d) ist eine konvexe Region und daher natürlich auch zusammenhängend.
Der offene Kern einer Region ist die Menge der inneren Punkte der Region.
Eine Region heißt offen, wenn der offene Kern einer Region die gesamte Region ist, wenn sie also nur aus inneren Punkten besteht.
Ein Schnitt zweier Regionen ist die Schnittmenge der beiden Regionen und selbst wieder eine Region.
Es sei
![]() eine Familie von
eine Familie von ![]() Regionen.
Regionen. ![]() ist
eine unabhängige Familie von Regionen, wenn die Regionen offen und
zusammenhängend sind, die Komplemente der Regionen zusammenhängend und jeder
Schnitt
ist
eine unabhängige Familie von Regionen, wenn die Regionen offen und
zusammenhängend sind, die Komplemente der Regionen zusammenhängend und jeder
Schnitt
![]() von Regionen existiert (also nicht leer
ist), wobei
von Regionen existiert (also nicht leer
ist), wobei ![]() entweder die Region
entweder die Region ![]() oder der offene Kern des
Komplements von
oder der offene Kern des
Komplements von ![]() ist.
ist.
Der Rahmen um die unabhängige Familie von Regionen im Venn-Diagramm bezeichnet
das sogenannte ,,Univers of Discurs``, und grenzt die unendliche Punktebene auf
einen kleinen Bereich ein, der nur die ![]() betrachteten Regionen enthält.
Dieses ist notwendig, damit die später noch einzuführende
Schraffierungsoperation auf den Regionen endlich ist.
betrachteten Regionen enthält.
Dieses ist notwendig, damit die später noch einzuführende
Schraffierungsoperation auf den Regionen endlich ist.
Einige Beispiele von Venn-Diagrammen:
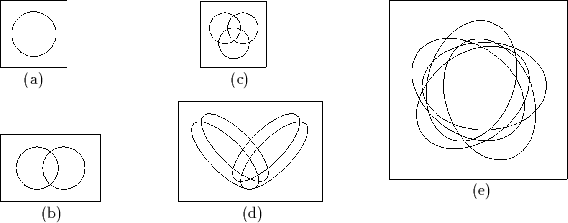
(a) ist ein Venn-Diagramm mit einer Region, (b) ein Venn-Diagramm mit zwei Regionen, (c) ein Venn-Diagramm mit drei Regionen, (d) ein Venn-Diagramm mit vier Regionen und (e) ein Venn-Diagramm mit fünf Regionen. Besonderes Kennzeichen dieser Diagramme ist, daß die verwendeten Regionen konvex sind.
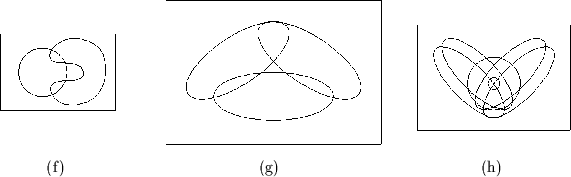
(f) zeigt kein Venn-Diagramm, denn zwei der Schnitte sind nicht zusammenhängend. (g) ist nicht einmal eine unabhängige Familie, denn der Schnitt der drei Regionen ist leer. (h) zeigt ein Diagramm mit fünf Regionen, das oft als Venn-Diagramm bezeichnet wird. Im Sinne der Definition 2.29 trifft das jedoch nicht zu, denn die fünfte Region ist ein Ring, das Komplement dieser Region daher nicht zusammenhängend.
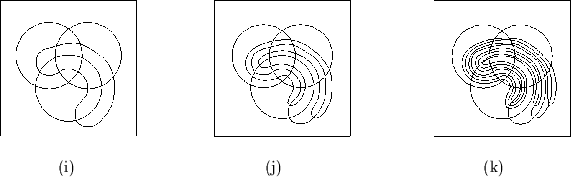
(i) zeigt ein weiteres Venn-Diagramm mit vier Regionen. Die vierte Region ist
aber nicht mehr konvex. Dieses Diagramm bildet den Ausgangspunkt einer ganzen
Reihe von Diagrammen. Gezeigt seien hier nur die Diagramme mit fünf (j) und
sechs (k) Regionen. Jedes Diagramm entsteht aus dem vorherigen, indem der Rand
der ![]() -1-ten Region in einer ,,schlauchförmigen`` neuen Region verpackt wird.
Diese Konstruktion läßt sich bis zu einem beliebigen
-1-ten Region in einer ,,schlauchförmigen`` neuen Region verpackt wird.
Diese Konstruktion läßt sich bis zu einem beliebigen ![]() fortsetzen,
allerdings gibt es bald zeichentechnische Probleme.
fortsetzen,
allerdings gibt es bald zeichentechnische Probleme.
Die ![]() Variablen
Variablen
![]() eines endlichen Booleschen Verbandes
seien in beliebiger, z.B. alphabetischer, aber letztlich fester Reihenfolge
geordnet. Dann wird jedem Minterm
eines endlichen Booleschen Verbandes
seien in beliebiger, z.B. alphabetischer, aber letztlich fester Reihenfolge
geordnet. Dann wird jedem Minterm
![]() für
für ![]() Variablen
in einem Venn-Diagramm mit einer unabhängigen Familie von
Variablen
in einem Venn-Diagramm mit einer unabhängigen Familie von ![]() Regionen
Regionen
![]() die Zelle zugeordnet, die sich als Schnitt von
die Zelle zugeordnet, die sich als Schnitt von ![]() Regionen
ergibt, wobei jeweils die Region
Regionen
ergibt, wobei jeweils die Region ![]() berücksichtigt wird, wenn
berücksichtigt wird, wenn ![]() ist, oder aber der offene Kern des Komplements von
ist, oder aber der offene Kern des Komplements von ![]() ,
wenn
,
wenn
![]() ist.
ist.
Beweis: Unterscheiden sich zwei Minterme für ![]() Variablen an mindestens
einer Stelle, so werden sie auch mit unterschiedlichen Zellen im Venn-Diagramm
identifiziert, da dann der Schnitt mit dem Komplement einer Region durchgeführt
wird und nicht mit der Region selbst (bzw. umgekehrt). Die Abbildung ist also
injektiv.
Variablen an mindestens
einer Stelle, so werden sie auch mit unterschiedlichen Zellen im Venn-Diagramm
identifiziert, da dann der Schnitt mit dem Komplement einer Region durchgeführt
wird und nicht mit der Region selbst (bzw. umgekehrt). Die Abbildung ist also
injektiv.
Die Definition des Venn-Diagrammes legt fest, daß für eine unabhängige
Familie von ![]() Regionen jeder der Schnitte
Regionen jeder der Schnitte
![]() eine offene zusammenhängende Region ist, wobei jedes
eine offene zusammenhängende Region ist, wobei jedes ![]() entweder
die (offene) Region
entweder
die (offene) Region ![]() oder der offene Kern des Komplements von
oder der offene Kern des Komplements von ![]() ist. Jedes der
ist. Jedes der ![]() kann also in den Schnitten
kann also in den Schnitten
![]() zwei Regionen darstellen. Daher gibt es rein kombinatorisch
mindestens
zwei Regionen darstellen. Daher gibt es rein kombinatorisch
mindestens ![]() verschiedene Zellen in einem Venn-Diagramm. Jeder dieser
Schnitte ist nach Definition zudem zusammenhängend, d.h., es gibt genau
verschiedene Zellen in einem Venn-Diagramm. Jeder dieser
Schnitte ist nach Definition zudem zusammenhängend, d.h., es gibt genau ![]() Zellen in einem Venn-Diagramm.
Zellen in einem Venn-Diagramm.
Daher ist für die Abbildung aus Definition 2.30 die Anzahl der Bilder (Zellen) gleich der Anzahl der Urbilder (Minterme), die Abbildung ist daher surjektiv, also insgesamt bijektiv.
Aufgrund der Zuordnung der Mintermvariablen zu den Regionen (Def. 2.30
und Satz 2.36), gibt es also eine eineindeutige Abbildung zwischen den
Zellen im Venn-Diagramm und den Mintermen Boolescher Funktionen für ![]() Variablen.
Variablen.
Um bestimmte Zellen zu markieren wird im folgenden ein Punkt in den betreffenden Zellen plaziert werden2.1
Nun wird eine Beziehung zwischen beliebigen Booleschen Funktionen und Mengen von Zellen hergestellt.
Seien ![]() und
und ![]() Boolesche Funktionen, die ein Grundobjekt repräsentieren.
Dann sind
Boolesche Funktionen, die ein Grundobjekt repräsentieren.
Dann sind ![]() und
und ![]() Mengen der Zellen, die in der jeweiligen Region
liegen, die das Grundobjekt
Mengen der Zellen, die in der jeweiligen Region
liegen, die das Grundobjekt ![]() bzw.
bzw. ![]() repräsentiert. Dann gilt:
repräsentiert. Dann gilt:
Mit dieser Definition haben wir die sogenannten Vennschen Umfangs-Diagramme definiert. Wir hätten genausogut sog. Inhalts-Diagramme definieren können. Im folgenden werden wir uns nur mit den Umfangs-Diagrammen beschäftigen, dieses also auch nicht mehr gesondert erwähnen. Wer sich für die Inhaltsdiagramme interessiert, sollte in [5] nachlesen.
Die in Definition 2.31 definierte Abbildung, genannt ,,![]() ``, zwischen
Booleschen Funktionen und Mengen von Zellen ist ein Isomorphismus.
``, zwischen
Booleschen Funktionen und Mengen von Zellen ist ein Isomorphismus.
Beweis: Es gilt:
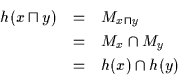
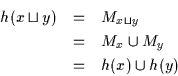
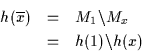
![]() ist also ein Homomorphismus. Aus dem Beweis von Satz 2.36 hat sich
ergeben, daß ein Venn-Diagramm mit einer unabhängigen Familie von
ist also ein Homomorphismus. Aus dem Beweis von Satz 2.36 hat sich
ergeben, daß ein Venn-Diagramm mit einer unabhängigen Familie von ![]() Regionen genau
Regionen genau ![]() Zellen enthält, die eineindeutig auf die
Zellen enthält, die eineindeutig auf die ![]() Minterme Boolescher Verbände für
Minterme Boolescher Verbände für ![]() Variablen abgebildet werden. Mehrere
Zellen können zu einem größeren Bereich zusammengefaßt werden. Dieses
entspricht nach Definition 2.31 der Disjunktion der entsprechenden
Minterme. Die gleiche Argumentation wie in Satz 2.30 führt dazu, daß
sich
Variablen abgebildet werden. Mehrere
Zellen können zu einem größeren Bereich zusammengefaßt werden. Dieses
entspricht nach Definition 2.31 der Disjunktion der entsprechenden
Minterme. Die gleiche Argumentation wie in Satz 2.30 führt dazu, daß
sich ![]() verschiedene Zellenkombinationen bilden lassen. Nach Satz
2.31 gibt es
verschiedene Zellenkombinationen bilden lassen. Nach Satz
2.31 gibt es ![]() verschiedene Boolesche Funktionen für
verschiedene Boolesche Funktionen für ![]() Variablen. Die Abbildung
Variablen. Die Abbildung ![]() ist also surjektiv, daher insgesamt bijektiv und
damit ein Isomorphismus.
ist also surjektiv, daher insgesamt bijektiv und
damit ein Isomorphismus.
Beweis: Wir bilden die Vereinigung von ![]() und
und ![]() (a) und vereinigen das
Ergebnis mit
(a) und vereinigen das
Ergebnis mit ![]() (b). Andererseits vereinige man
(b). Andererseits vereinige man ![]() mit der Vereinigung von
mit der Vereinigung von ![]() und
und ![]() (c). Das Ergebnis (d) ist identisch mit (b).
(c). Das Ergebnis (d) ist identisch mit (b).
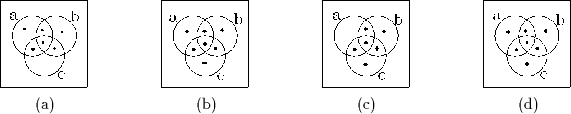
Damit ist (V1a) bewiesen. Nun bilden wir den Schnitt von ![]() und
und ![]() (e) und
schneiden das Ergebnis mit
(e) und
schneiden das Ergebnis mit ![]() (f). Andererseits schneide man
(f). Andererseits schneide man ![]() mit dem
Schnitt von
mit dem
Schnitt von ![]() und
und ![]() (g). Das Ergebnis (h) ist identisch mit (f).
(g). Das Ergebnis (h) ist identisch mit (f).
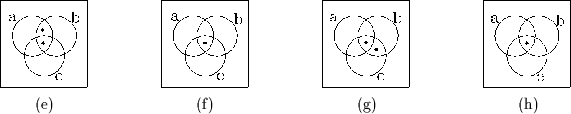
Damit ist (V1b) bewiesen. Es ist im Venn-Diagramm völlig beliebig, ob der
Schnitt von ![]() und
und ![]() oder der Schnitt von
oder der Schnitt von ![]() und
und ![]() gebildet wird.
Betroffen ist (sind) immer die gleiche(n) Zelle(n). Ebensolches gilt für die
Vereinigung von
gebildet wird.
Betroffen ist (sind) immer die gleiche(n) Zelle(n). Ebensolches gilt für die
Vereinigung von ![]() und
und ![]() und die Vereinigung von
und die Vereinigung von ![]() und
und ![]() .
Damit sind auch
(V2a) und (V2b) erledigt.
.
Damit sind auch
(V2a) und (V2b) erledigt.
Schneidet man ![]() mit der Vereinigung von
mit der Vereinigung von ![]() und
und ![]() ,
so bleiben die Zellen von
,
so bleiben die Zellen von
![]() ,
womit (V3a) bewiesen ist. Vereinigt man
,
womit (V3a) bewiesen ist. Vereinigt man ![]() mit dem Schnitt von
mit dem Schnitt von ![]() und
und
![]() ,
so bleiben die Zellen von
,
so bleiben die Zellen von ![]() ,
daher ist auch (V3b) bewiesen.
,
daher ist auch (V3b) bewiesen.
Schneidet man ![]() mit der Vereinigung von
mit der Vereinigung von ![]() und
und ![]() (i), so ist das Ergebnis
(j). Vereinigt man den Schnitt von
(i), so ist das Ergebnis
(j). Vereinigt man den Schnitt von ![]() und
und ![]() (k) mit dem Schnitt von
(k) mit dem Schnitt von ![]() und
und
![]() (l), so ist das Ergebnis (m) identisch mit (j).
(l), so ist das Ergebnis (m) identisch mit (j).

Damit ist (V4a) bewiesen. Vereinigt man ![]() mit dem Schnitt von
mit dem Schnitt von ![]() und
und ![]() (n),
so ist das Ergebnis (o). Schneidet man die Vereinigung von
(n),
so ist das Ergebnis (o). Schneidet man die Vereinigung von ![]() und
und ![]() (p) mit
der Vereinigung von
(p) mit
der Vereinigung von ![]() und
und ![]() (q), so ist das Ergebnis (r) identisch mit (o).
(q), so ist das Ergebnis (r) identisch mit (o).

Damit ist (V4b) bewiesen. Die leere Menge vereinigt mit den Zellen von ![]() ergibt die Zellen von
ergibt die Zellen von ![]() .
D.h. es ist
.
D.h. es ist
![]() .
Daher ist die leere
Punktmenge das Null-Objekt. Das gesamte Diagramm
.
Daher ist die leere
Punktmenge das Null-Objekt. Das gesamte Diagramm ![]() geschnitten mit den
Zellen, die
geschnitten mit den
Zellen, die ![]() repräsentieren, ergibt wieder die Zellen von
repräsentieren, ergibt wieder die Zellen von ![]() .
D.h. es ist
.
D.h. es ist
![]() .
Daher ist
.
Daher ist ![]() das Eins-Objekt. Das Innere der Region, die
das Eins-Objekt. Das Innere der Region, die
![]() repräsentiert, vereinigt mit dem offenen Kern des Komplements der von
repräsentiert, vereinigt mit dem offenen Kern des Komplements der von ![]() repräsentierten Region ergibt nach Definition das gesamte Diagramm, ist also
repräsentierten Region ergibt nach Definition das gesamte Diagramm, ist also
![]() .
Das Innere der Region, die
.
Das Innere der Region, die ![]() repräsentiert, geschnitten mit dem offenen
Kern des Komplements der
repräsentiert, geschnitten mit dem offenen
Kern des Komplements der ![]() repräsentierenden Region ergibt nach Definition
der Diagramme den leeren Schnitt, ist also
repräsentierenden Region ergibt nach Definition
der Diagramme den leeren Schnitt, ist also ![]() .
Daher erfüllt der offene Kern
des Komplements der
.
Daher erfüllt der offene Kern
des Komplements der ![]() repräsentierenden Region die Bedingungen der Booleschen
Komplementdefinition. Eine vergleichbare Form der Substitutionsregel gilt,
zumindest auf dieser Stufe der Einführung der Venn-Diagramme, auch im
Hintergrund der Diagramme. Wie sonst hätte man auch die Booleschen Gleichungen
bearbeiten können. Ein Beweis der Substitutionsregel ist daher nicht notwendig.
repräsentierenden Region die Bedingungen der Booleschen
Komplementdefinition. Eine vergleichbare Form der Substitutionsregel gilt,
zumindest auf dieser Stufe der Einführung der Venn-Diagramme, auch im
Hintergrund der Diagramme. Wie sonst hätte man auch die Booleschen Gleichungen
bearbeiten können. Ein Beweis der Substitutionsregel ist daher nicht notwendig.
Ein endlicher Boolescher Verband mit ![]() Variablen ist isomorph mit einem
Venn-Diagramm mit einer unabhängigen Familie von
Variablen ist isomorph mit einem
Venn-Diagramm mit einer unabhängigen Familie von ![]() Regionen.
Regionen.
Beweis: Mit dem Beweis von Satz 2.38 ist gezeigt, daß sich mit Venn-Diagrammen alles machen läßt, was in endlichen Booleschen Verbänden möglich ist. Umgekehrt zeigte der Beweis von Satz 2.37 die Isomorphie des Booleschen Verbandes mit den Venn-Diagrammen. Weitere Axiome haben die Venn-Diagramme in dem Sinne nicht.
Mit Kreisen können nur Venn-Diagramme bis ![]() erzeugt werden. Mit Ellipsen
kann man bis
erzeugt werden. Mit Ellipsen
kann man bis ![]() kommen. Siehe dazu [3].
kommen. Siehe dazu [3].
Beweis: Für ein zusammenhängendes Netz in der Ebene gilt der Euler Satz:
wobei ![]() die Zahl der Schnittpunkte,
die Zahl der Schnittpunkte, ![]() die Zahl der Kanten und
die Zahl der Kanten und ![]() die
Zahl der Zellen ist, die durch das Netz in der Ebene erzeugt werden.
die
Zahl der Zellen ist, die durch das Netz in der Ebene erzeugt werden.
Das Netz werde durch die Ränder einer unabhängigen Familie von ![]() Regionen
erzeugt, wie sie für Venn-Diagramme definiert sind. Es können
Regionen
erzeugt, wie sie für Venn-Diagramme definiert sind. Es können ![]() Regionen-Paare aus den
Regionen-Paare aus den ![]() Regionen kombiniert werden. Schneiden sich je 2
Regionen-Ränder in
Regionen kombiniert werden. Schneiden sich je 2
Regionen-Ränder in ![]() Punkten, und haben keine 3 Regionen-Ränder einen
gemeinsamen Punkt, so hat das Netz
Punkten, und haben keine 3 Regionen-Ränder einen
gemeinsamen Punkt, so hat das Netz
![]() Schnittpunkte
und
Schnittpunkte
und ![]() Kanten. Dann vereinfacht sich der Euler-Satz zu:
Kanten. Dann vereinfacht sich der Euler-Satz zu:
Für ein Venn-Diagramm ist ![]() .
Daher gilt:
.
Daher gilt:
Einsetzen der Ergebnisse für Schnittpunkte und Kanten ergibt:
Umgeformt nach ![]() ergibt sich:
ergibt sich:
Die Ränder zweier kreisförmiger Regionen schneiden sich in maximal 2 Punkten,
die Ränder zweier ellipsenförmiger Regionen in maximal 4 Punkten. ![]() ist also
für Kreise gleich 2 und obige Formel ist erfüllbar für
ist also
für Kreise gleich 2 und obige Formel ist erfüllbar für ![]() .
Für Ellipsen
ist
.
Für Ellipsen
ist ![]() gleich 4, und obige Formel ist erfüllbar für
gleich 4, und obige Formel ist erfüllbar für ![]() .
.