
Nächste Seite: 2.2 Bemerkungen zum Hintergrundkalkül
Aufwärts: 2. Grundlagen
Vorherige Seite: 2. Grundlagen
Unterabschnitte
Definition 2.1 (Bereich
)
Ein Bereich enthält Objekte, die in irgendeiner Weise definiert sind,
welche im folgenden nicht weiter wichtig ist.
Diese Objekte seien mit
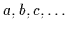 als Variablen bezeichnet und dürfen sowohl überstrichen als auch indiziert
sein. Zusätzlich wird angenommen, daß ein Bereich mindestens ein Objekt
enthält.
als Variablen bezeichnet und dürfen sowohl überstrichen als auch indiziert
sein. Zusätzlich wird angenommen, daß ein Bereich mindestens ein Objekt
enthält.
Die später behandelten Varianten von Verbänden werden mindestens ein Objekt
enthalten, zuvor wird es die Beweise vereinfachen. Diese Definition ist für den
augenblicklichen Bedarf etwas zu weit konzipiert, im weiteren Verlauf werden
diese Erweiterungen jedoch benötigt.
Zunächst aber zur Theorie der Verbände, die hier nur soweit entwickelt werden
soll, wie es zur Behandlung der Venn-Diagramme nötig ist. Dazu wurden im
wesentlichen [1] und [2] verwendet.
Definition 2.2 (Abgeschlossene Verknüpfung
)
Eine beliebigstellige Verknüpfung 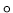 heißt abgeschlossen über dem
Bereich
heißt abgeschlossen über dem
Bereich 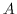 ,
wenn für alle
,
wenn für alle
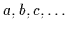 ,
auch
,
auch
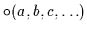 in
in 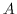 ist.
ist.
Definition 2.3 (Algebraische Struktur
)
Ein Bereich 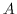 mit einer oder mehreren abgeschlossenenen Verknüpfungen heißt
algebraische Struktur:
mit einer oder mehreren abgeschlossenenen Verknüpfungen heißt
algebraische Struktur:
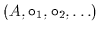 .
.
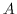 heißt
Trägerbereich dieser Struktur.
heißt
Trägerbereich dieser Struktur.
Wenn im folgenden also auf Objekte
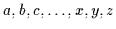 bezug genommen
wird, so sind immer Objekte aus dem Bereich gemeint.
bezug genommen
wird, so sind immer Objekte aus dem Bereich gemeint.
Definition 2.4 (Verband
)
Die algebraische Struktur
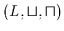 heißt Verband, wenn
folgende Bedingungen für alle Variablen
heißt Verband, wenn
folgende Bedingungen für alle Variablen 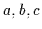 aus dem Bereich
aus dem Bereich 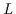 erfüllt
sind:
erfüllt
sind:
| (V1a) |
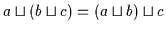 |
| (V1b) |
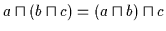 |
| (V2a) |
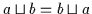 |
| (V2b) |
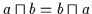 |
| (V3a) |
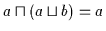 |
| (V3b) |
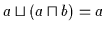 |
Bemerkung 2.1 (Substitutionsregel
)
Ein Objekt aus dem Bereich wird auch Term genannt, ebenso alle Objekte,
die sich durch Verknüpfung mittels 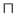 oder
oder 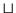 erzeugen lassen.
Terme werden mittels des Gleichheitszeichens = in Beziehung zueinander gesetzt.
Für dieses Zeichen gilt unter anderem die Substitutionsregel, die besagt, daß
Terme, die in der Gleichheitsbeziehung zueinander stehen, wechselseitig in und
füreinander eingesetzt (substituiert) werden dürfen. Die Gleichheit ist eine
Äquivalenzrelation, also symmetrisch, transitiv und auch reflexiv.
erzeugen lassen.
Terme werden mittels des Gleichheitszeichens = in Beziehung zueinander gesetzt.
Für dieses Zeichen gilt unter anderem die Substitutionsregel, die besagt, daß
Terme, die in der Gleichheitsbeziehung zueinander stehen, wechselseitig in und
füreinander eingesetzt (substituiert) werden dürfen. Die Gleichheit ist eine
Äquivalenzrelation, also symmetrisch, transitiv und auch reflexiv.
Satz 2.1 (Dualitätsprinzip für Verbände
)
Der duale Ausdruck eines Satzes der Verbandstheorie ist wieder ein Satz der
Verbandstheorie.
Beweis: Für jedes Axiom ist auch dessen dualer Ausdruck ein Axiom, daher
kann für jeden aus den Axiomen erzeugten Ausdruck auch dessen dualer Ausdruck
aus den Axiomen erzeugt werden.
Satz 2.2 (Idempotenz
)
Sei
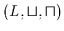 ein Verband. Dann gilt für alle
ein Verband. Dann gilt für alle 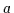 :
:
(a)
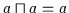
(b)
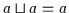
Beweis: (a) Es ist
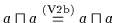 .
Ersetzen des rechten
.
Ersetzen des rechten 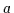 auf der rechten Seite der Gleichung nach (V3b) durch
auf der rechten Seite der Gleichung nach (V3b) durch
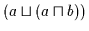 ergibt
ergibt
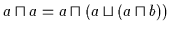 .
Anwendung von (V3a) ergibt
.
Anwendung von (V3a) ergibt
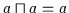 .
.
Der Beweis für (b) ergibt sich unmittelbar durch Anwendung des
Dualitätsprinzips.
Satz 2.3
In jedem Verband
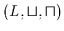 gilt für alle
gilt für alle 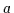 und
und 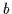 :
:
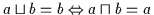
Beweis: ,,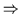 `` Es ist
`` Es ist
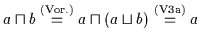 .
.
,,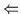 `` Es ist
`` Es ist
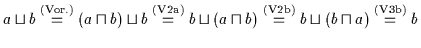 .
.
Satz 2.4
In jedem Verband
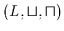 gilt für alle
gilt für alle 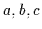 :
:
(a)
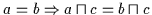
(b)
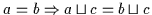
Beweis: (a) Es ist
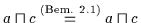 .
Mit
.
Mit 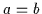 gilt dann:
gilt dann:
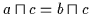 .
.
(b) Der Beweis verläuft analog.
Satz 2.5
In jedem Verband gibt es höchstens ein Nullobjekt und höchstens ein
Einsobjekt.
Beweis: Sind 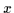 und
und 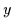 zwei Nullobjekte, so gilt
zwei Nullobjekte, so gilt
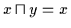 ( da
( da
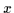 Nullobjekt ) und
Nullobjekt ) und
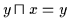 ( da
( da 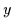 Nullobjekt ), also ist
Nullobjekt ), also ist
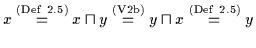 .
Der Beweis für das Einsobjekt
verläuft analog mit den dualen Ausdrücken.
.
Der Beweis für das Einsobjekt
verläuft analog mit den dualen Ausdrücken.
Bemerkung 2.3
Da es nur höchstens ein Null- und höchstens ein Einsobjekt in einem Verband
geben kann, seinen diese (falls vorhanden) mit 0 bzw. 1 bezeichnet. Die
Bedingungen für Nullobjekt und Einsobjekt sind dual zueinander definiert. Daher
ist (falls beide vorhanden) die 0 das Dual der 1 und umgekehrt. Für einen
solchen Verband wird die Dualisierungsregel dementsprechend erweitert.
In der Verbandstheorie spielen neben den Verbänden die Halbordnungsstrukturen
eine große Rolle.
Satz 2.6 (Dualitätsprinzip für Halbordnungsstrukturen)
Der duale Ausdruck eines Satzes der Theorie der Halbordnungsstrukturen ist
ebenfalls ein Satz dieser Theorie.
Beweis: Jedes Axiom ist selbstdual (bis auf Umbenennung der Variablen),
daher kann man zu jedem aus den Axiomen hergeleiteten Satz der Theorie der
Halbordnungsstrukturen der duale Ausdruck ebenfalls abgeleitet werden.
Satz 2.7
Es gibt in einer Halbordnungsstruktur höchstens ein kleinstes Objekt und
höchstens ein größtes Objekt.
Beweis: Seien 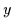 und
und 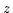 kleinste Objekte. Dann gilt
kleinste Objekte. Dann gilt
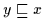 für alle
für alle 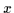 ,
insbesondere gilt also auch
,
insbesondere gilt also auch
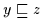 .
Mit der gleichen
Argumentation gilt
.
Mit der gleichen
Argumentation gilt
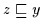 ,
nach (H2) also
,
nach (H2) also 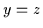 .
Der Beweis für
größte Objekte verläuft analog mit den dualen Ausdrücken.
.
Der Beweis für
größte Objekte verläuft analog mit den dualen Ausdrücken.
Satz 2.8
Sei 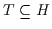 .
Dann gibt es höchstens ein Supremum (Infimum) von
.
Dann gibt es höchstens ein Supremum (Infimum) von 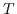 .
.
Beweis: Seien 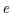 und
und 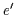 zwei Suprema (Infima) von
zwei Suprema (Infima) von 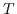 .
Dann sind beide
insbesondere auch obere (untere) Schranken von
.
Dann sind beide
insbesondere auch obere (untere) Schranken von 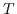 (Def 2.10). Dann gilt
(Def 2.10). Dann gilt
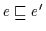 und
und
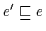 ,
d.h. nach (H2):
,
d.h. nach (H2): 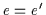 .
.
Bemerkung 2.6
Wir wollen uns im folgenden auf Halbordnungsstrukturen beschränken, in denen
Suprema und Infima von Objekten eines Bereiches immer existieren und mit zu dem
Bereich gehören. 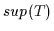 und
und 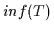 sind zueinander
dual definiert. Die Dualisierungsregel für Halbordnungsstrukturen ist
dementsprechend zu erweitern.
sind zueinander
dual definiert. Die Dualisierungsregel für Halbordnungsstrukturen ist
dementsprechend zu erweitern.
Beweis: (a) Nach Definition 2.9 ist
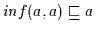 .
Andererseits gilt aber
.
Andererseits gilt aber
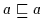 ,
d.h.
,
d.h. 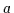 ist untere Schranke von
ist untere Schranke von
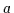 .
.
Da 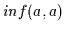 nach Definition 2.10 die größte untere Schranke von
nach Definition 2.10 die größte untere Schranke von
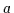 und
und 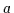 ist, gilt
ist, gilt
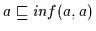 .
Nach (H2) gilt damit
.
Nach (H2) gilt damit
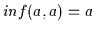 .
.
(b) Der Beweis ist dual zu dem von (a).
Die Beweise lassen sich einfach auf mehr als zwei Komponenten erweitern.
Satz 2.10
Es gilt:
(a)
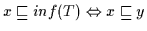 für alle
für alle 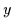 aus
aus 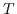 .
.
(b)
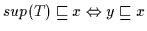 für alle
für alle 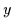 aus
aus 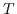 .
.
Beweis: (a) ,,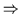 `` Nach Definition 2.9 ist das Infimum
eine untere Schranke, daß heißt es gilt
`` Nach Definition 2.9 ist das Infimum
eine untere Schranke, daß heißt es gilt
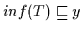 für alle
für alle
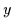 aus
aus 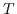 .
Nach Voraussetzung gilt
.
Nach Voraussetzung gilt
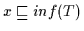 ,
daher gilt
nach Axiom (H3):
,
daher gilt
nach Axiom (H3):
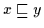 für alle
für alle 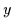 aus
aus 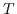 .
.
,,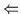 `` Umgekehrt folgt aus
`` Umgekehrt folgt aus
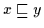 für alle
für alle 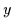 aus
aus 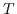 ,
daß
,
daß 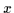 untere Schranke von
untere Schranke von 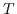 ist, nach Definition 2.10 gilt dann
aber
ist, nach Definition 2.10 gilt dann
aber
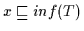 .
.
(b) Der Beweis ist dual zu (a).
Beweis: (a) Nach Voraussetzung ist
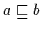 .
Außerdem gilt
.
Außerdem gilt
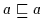 (H1), daher gilt nach Satz 2.10
(H1), daher gilt nach Satz 2.10
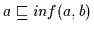 .
Nach Definition 2.9 gilt auch
.
Nach Definition 2.9 gilt auch
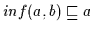 ,
daher gilt nach (H2)
,
daher gilt nach (H2) 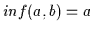 .
.
(b) Der Beweis ist dual zu (a).
Beweis: Nach Satz 2.11 folgt aus
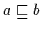 :
:
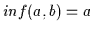 ,
damit auch (Beweis von Satz 2.11)
,
damit auch (Beweis von Satz 2.11)
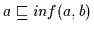 .
Da
.
Da
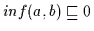 folgt
daher nach (H3)
folgt
daher nach (H3)
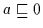 .
.
Nun werden Verband- und Halbordnungsstruktur zueinander in Beziehung gesetzt.
Beweis: (1) Aus Satz 2.2 (
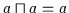 )
folgt nach der
Definition aus Satz 2.13:
)
folgt nach der
Definition aus Satz 2.13:
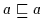 .
.
(2) Aus
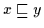 und
und
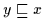 folgt zunächst nach obiger
Definition
folgt zunächst nach obiger
Definition
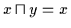 und
und
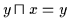 ,
daher gilt:
,
daher gilt:
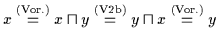 .
.
(3) Aus
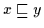 und
und
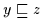 folgt zunächst nach
Definition
folgt zunächst nach
Definition
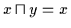 und
und
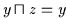 .
Dann ist durch Einsetzen
.
Dann ist durch Einsetzen
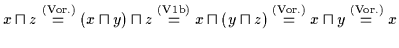 ,
also
,
also
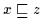 .
.
Satz 2.14
Seien
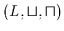 ein Verband und
ein Verband und
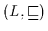 eine wie vor
definierte Halbordnungsstruktur. Dann gilt für alle
eine wie vor
definierte Halbordnungsstruktur. Dann gilt für alle 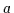 und
und 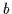 :
:
(a)
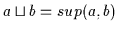
(b)
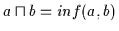
Falls Verband wie Halbordnungsstruktur über 0/1 bzw. 0
 /1
/1
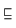 verfügen, gilt:
verfügen, gilt:
(c)
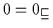
(d)
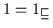
Beweis: (a) Nach (V3a) gilt
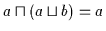 und
und
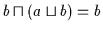 ,
was nach obiger Definition mit
,
was nach obiger Definition mit
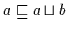 sowie
sowie
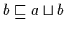 gleichbedeutend ist; somit ist
gleichbedeutend ist; somit ist 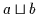 obere Schranke von
obere Schranke von 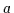 und
und 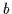 .
.
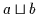 ist aber auch die kleinste obere Schranke. Ist nämlich
ist aber auch die kleinste obere Schranke. Ist nämlich
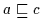 und
und
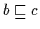 ,
so ist
,
so ist
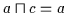 und
und
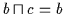 ,
sowie nach Satz 2.3
,
sowie nach Satz 2.3
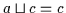 und
und
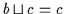 .
Daher ist
.
Daher ist
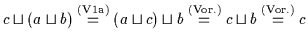 und
daher (Satz 2.3) ist wiederum nach obiger Definition
und
daher (Satz 2.3) ist wiederum nach obiger Definition
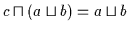 ,
was gleichwertig mit
,
was gleichwertig mit
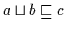 ist.
ist.
(b) Der Beweis ist dual zu (a).
(c) Nach Definition 2.5 gilt im Verband für das Nullobjekt 0 für alle
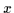 :
:
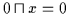 .
Nach Satz 2.13 gilt daher
.
Nach Satz 2.13 gilt daher
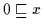 für
alle
für
alle 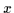 ,
daher ist die 0 ein kleinstes Objekt im Sinne von Definition
2.8. Daher gilt:
,
daher ist die 0 ein kleinstes Objekt im Sinne von Definition
2.8. Daher gilt:
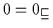
(d) Der Beweis ist dual zu (c).
Sei nun umgekehrt eine Halbordnungsstruktur
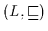 vorgegeben. Es
sollen nun zwei abgeschlossene Verknüpfungen
vorgegeben. Es
sollen nun zwei abgeschlossene Verknüpfungen 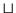 und
und 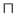 definiert
werden, so daß
definiert
werden, so daß
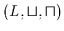 einen Verband darstellt.
einen Verband darstellt.
Beweis: (1) Nach Definition 2.10 sind Suprema bzw. Infima bereits
kommutativ definiert, nach Übersetzung sind daher (V2a) und (V2b) bewiesen.
(2) Es ist nach Definition 2.10
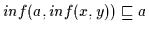 und
und
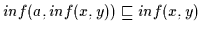 .
Weiterhin ist
nach Definition 2.10
.
Weiterhin ist
nach Definition 2.10
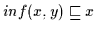 und
und
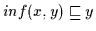 .
Daher gilt nach (H3)
.
Daher gilt nach (H3)
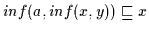 und
und
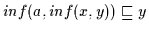 .
Daraus folgt nach
Definition 2.10, daß
.
Daraus folgt nach
Definition 2.10, daß
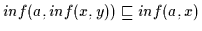 und
und
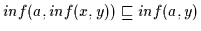 gilt.
Das ergibt wiederum nach Definition 2.10, daß
gilt.
Das ergibt wiederum nach Definition 2.10, daß
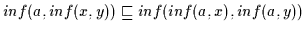 gilt.
gilt.
Umgekehrt gilt nach Def. 2.10
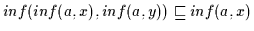 und
und
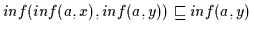 .
Ebenso ist nach
Def. 2.10
.
Ebenso ist nach
Def. 2.10
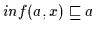 ;
;
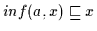 ;
;
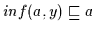 und
und
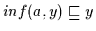 .
.
Daher gilt
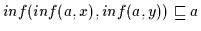 ;
;
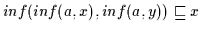 ;
;
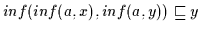 nach (H3). Daher
ist nach Definition
2.10
nach (H3). Daher
ist nach Definition
2.10
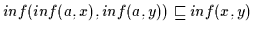 und damit ist nach
Definition 2.10 auch
und damit ist nach
Definition 2.10 auch
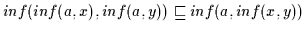 .
.
Daher ist
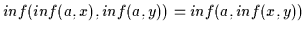 nach (H2).
nach (H2).
Das kann man ebenso für
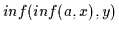 durchführen, woraus
sich ergibt:
durchführen, woraus
sich ergibt:
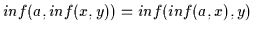 .
Das
bedeutet, daß nach Übersetzung
.
Das
bedeutet, daß nach Übersetzung
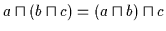 gilt, womit (V1b) bewiesen ist. Der Beweis von (V1a) verläuft dual.
gilt, womit (V1b) bewiesen ist. Der Beweis von (V1a) verläuft dual.
(3) Es gilt nach Definition 2.10
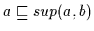 ,
daher
gilt nach Satz 2.11
,
daher
gilt nach Satz 2.11
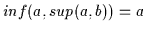 .
Ebenso gilt nach
Definition 2.10
.
Ebenso gilt nach
Definition 2.10
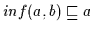 ,
daher gilt nach Satz
2.11
,
daher gilt nach Satz
2.11
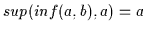 .
Damit sind nach Übersetzung
(V3a) und (V3b) bewiesen.
.
Damit sind nach Übersetzung
(V3a) und (V3b) bewiesen.
(4) Es sei
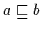 .
Nach Satz 2.11 gilt
.
Nach Satz 2.11 gilt 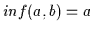 .
Nach Übersetzung gemäß Satz 2.14 gilt dann
.
Nach Übersetzung gemäß Satz 2.14 gilt dann
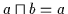 .
.
Für Null- und Einsobjekt gilt die Argumentation wie im Beweis von Satz
2.14.
Damit ist eine eindeutige Beziehung zwischen den Verbänden und den hier
betrachteten Halbordnungsstrukturen hergestellt. Es ist üblich, Verbände mit
den Halbordnungsstrukturen zu identifizieren, bei denen zu zwei Objekten aus
dem Trägerbereich der Halbordnungsstruktur auch deren Supremum und Infimum zu
dem Trägerbereich gehört. Alle Sätze, die für 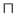 und
und 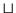 bewiesen
wurden, gelten daher auch für
bewiesen
wurden, gelten daher auch für 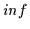 und
und 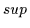 und umgekehrt. Die
Dualisierungsprinzipien beider Strukturen können ebenfalls ineinander
überführt bzw. ergänzt werden.
und umgekehrt. Die
Dualisierungsprinzipien beider Strukturen können ebenfalls ineinander
überführt bzw. ergänzt werden.
Beweis:
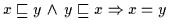 ist Axiom (H2). Es ist
ist Axiom (H2). Es ist
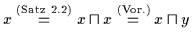 .
Dann gilt nach Satz 2.13
.
Dann gilt nach Satz 2.13
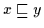 .
Umgekehrt ist
.
Umgekehrt ist
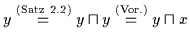 .
Dann gilt nach Satz 2.13
.
Dann gilt nach Satz 2.13
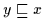 .
.
Die Booleschen Verbände sind das eigentliche Ziel dieses Kapitels, zunächst
erfolgen aber noch einige weitere einleitende Definitionen, Sätze und Beweise.
Definition 2.11 (Distributiver Verband
)
Ein Verband
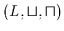 heißt genau dann distributiv, wenn für
alle
heißt genau dann distributiv, wenn für
alle 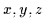 gilt:
gilt:
| (V4a) |
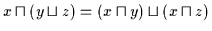 |
| (V4b) |
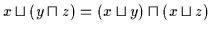 |
Man gibt zwei Distributivgesetze an, um die Gleichwertigkeit von 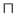 und
und
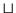 und damit die Dualität zu erhalten.
und damit die Dualität zu erhalten.
Satz 2.17 (Kürzungsregel
)
Ist
 ein distributiver Verband, dann gilt für alle
ein distributiver Verband, dann gilt für alle 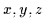 :
:
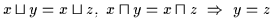 .
.
Beweis: Es ist:
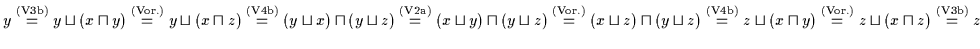 .
.
Satz 2.18
In einem distributiven Verband gibt es zu jedem Objekt höchstens ein
Komplement.
Beweis: Sind 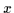 und
und 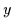 Komplemente von
Komplemente von 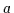 ,
so gilt gemäß Definition
2.12:
,
so gilt gemäß Definition
2.12:
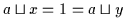 ,
sowie
,
sowie
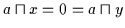 .
.
Dann ist
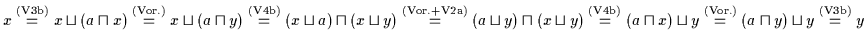 .
.
Satz 2.19 (Doppelte Negation
)
In einem distributiven Verband ist das Komplement des Komplementes eines
Objektes wieder das Objekt.
Beweis: Sei 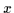 das Komplement von
das Komplement von 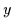 .
Dann gilt nach Definition
2.12:
.
Dann gilt nach Definition
2.12:
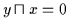 und
und
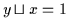 .
Sei ebenso
.
Sei ebenso 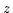 das
Komplement von
das
Komplement von 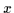 .
Dann gilt gemäß Definition 2.12:
.
Dann gilt gemäß Definition 2.12:
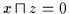 und
und
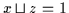 .
Insbesondere gilt also auch
.
Insbesondere gilt also auch
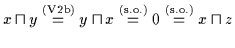 und
und
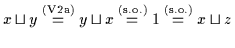 .
Da der Verband distributiv
ist, darf Satz 2.17 angewendet werden, so daß sich
.
Da der Verband distributiv
ist, darf Satz 2.17 angewendet werden, so daß sich 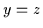 ergibt.
ergibt.
Definition 2.13 (Boolescher Verband
)
Ein Verband mit 0 und 1, der sowohl komplementär als auch distributiv ist,
heißt Boolescher Verband oder auch Boolesche Algebra.
Bemerkung 2.7 (Boolescher Verband
)
Für einen Booleschen Verband gelten also insgesamt die folgenden Axiome:
Abgeschlossenheit bezüglich der Operationen 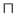 und
und 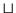 .
.
| (V1a) |
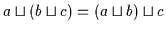 |
| (V1b) |
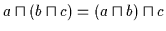 |
| (V2a) |
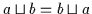 |
| (V2b) |
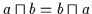 |
| (V3a) |
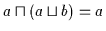 |
| (V3b) |
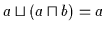 |
| (V4a) |
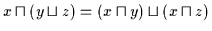 |
| (V4b) |
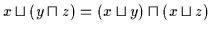 |
Es gibt ein kleinstes Objekt 0 und es gilt für alle 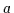 :
:
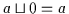 und
und
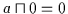 .
.
Es gibt ein größtes Objekt 1 und es gilt für alle 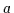 :
:
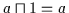 und
und
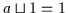 .
.
Für jedes Objekt 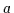 gibt es ein eindeutiges Komplement, das mit
gibt es ein eindeutiges Komplement, das mit 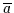 bezeichnet wird.
bezeichnet wird.
Es gilt
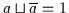 und
und
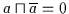 .
.
Bemerkung 2.8
Die Axiome des Booleschen Verbandes sind nicht unabhängig, (V1a),
(V1b), (V3a) und (V3b) sind z.B. aus den anderen Axiomen
herleitbar, die eindeutige Negation ergibt sich aus (V4a) und (V4b).
Zur besseren Unterscheidung wird der Boolesche Gleichungskalkül mit dem Kürzel
BV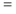 bezeichnet.
bezeichnet.
Mit dem Wort Variable wird ein beliebiges unbestimmtes Objekt aus dem
Trägerbereich bezeichnet. Eindeutig bestimmte Objekte, wie z.B. 0 und 1 werden
als Konstanten bezeichnet.
Ausdrücke wie z.B. 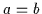 in Booleschen Verbänden oder
in Booleschen Verbänden oder
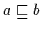 in
Halbordnungsstrukturen werden auch Formeln genannt.
in
Halbordnungsstrukturen werden auch Formeln genannt.
Bisher wurde nur bewiesen, daß die Axiomensysteme V1-V3 (der Gleichungskalkül)
und H1-H3 (der Halbordnungskalkül) äquivalent sind. Was ist mit BV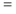 ?
Zumindest weiß man, daß man (nach Satz 2.15) in Halbordnungsstrukturen
?
Zumindest weiß man, daß man (nach Satz 2.15) in Halbordnungsstrukturen
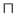 und
und 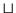 statt inf bzw. sup verwenden kann.
statt inf bzw. sup verwenden kann.
Beweis: (a) Es ist
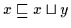 und
und
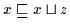 .
Daher ist nach Definition 2.10
.
Daher ist nach Definition 2.10
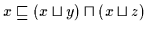 .
Es ist
.
Es ist
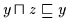 und
und
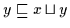 .
Daher gilt (H3)
.
Daher gilt (H3)
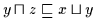 .
Außerdem ist
.
Außerdem ist
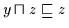 und
und
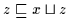 ,
daher nach (H3)
,
daher nach (H3)
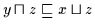 .
Daher gilt nach Definition 2.10
.
Daher gilt nach Definition 2.10
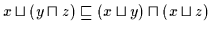 .
.
(b) Der Beweis ist dual zu (a).
Es fehlen die anderen Richtungen der Distributivgesetze. Diese fügen wir als
Axiome H4 hinzu:
| (H4) |
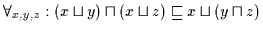 |
| |
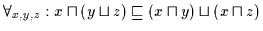 |
(H5) sei die Definition der größten/kleinsten Objekte gemäß Definition
2.8. (H6) sei die Definition des Komplements gemäß Definition
2.12 lediglich nun mit Hilfe von Satz 2.14 auf die
Halbordnungsstruktur bezogen.
Aus Satz 2.20 und (H4) folgt mittels (H2) sofort (V4). Umgekehrt folgt
aus (V4) mittels Satz 2.16 sofort (H4). Dieser Boolesche
Halbordnungskalkül ( H1 - H6 ) wird mit BV
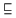 bezeichnet.
bezeichnet.
Satz 2.21
Sei
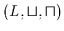 ein Boolescher Verband. Dann gilt:
ein Boolescher Verband. Dann gilt:
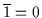 und
und
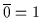 .
.
Beweis: Für das Komplement 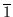 von
von 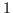 muß gelten:
muß gelten:
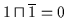 und
und
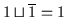 .
.
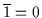 erfüllt
diese Bedingungen, denn es ist
erfüllt
diese Bedingungen, denn es ist
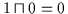 und
und
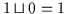 .
Für das
Komplement
.
Für das
Komplement 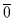 von
von 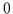 muß gelten:
muß gelten:
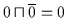 und
und
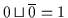 .
.
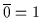 erfüllt diese Bedingungen, denn
es ist
erfüllt diese Bedingungen, denn
es ist
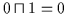 und
und
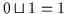 .
.
Beweis: (a) ,,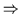 `` Es gilt
`` Es gilt
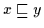 .
Dann gilt
nach Satz 2.13
.
Dann gilt
nach Satz 2.13
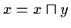 .
Dann ist
.
Dann ist
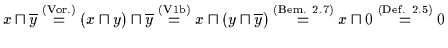 .
.
,,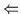 `` Es ist
`` Es ist
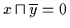 .
Dann gilt:
.
Dann gilt:
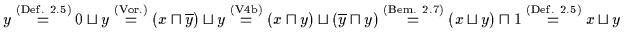 .
Dann gilt nach Satz
2.3
.
Dann gilt nach Satz
2.3
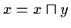 und daraus folgt nach Satz 2.13
und daraus folgt nach Satz 2.13
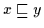 .
.
(b) ,,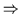 `` Es gilt
`` Es gilt
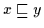 .
Dann gilt nach Satz
2.13
.
Dann gilt nach Satz
2.13
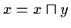 und nach Satz 2.3 gilt dann
und nach Satz 2.3 gilt dann
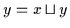 .
Dann ist
.
Dann ist
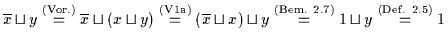 .
.
,, `` Es ist
`` Es ist
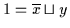 .
Dann gilt:
.
Dann gilt:
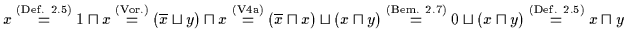 .
Nach Satz 2.13 gilt
dann:
.
Nach Satz 2.13 gilt
dann:
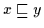 .
.
Satz 2.23 (De Morgan
)
Sei
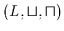 ein Boolescher Verband. Dann gilt für alle
ein Boolescher Verband. Dann gilt für alle 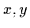 :
:
(a)
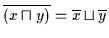
(b)
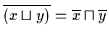
Beweis: (a) Es ist
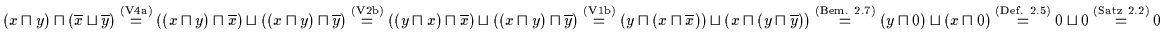 .
Daraus folgt nach Satz 2.22:
.
Daraus folgt nach Satz 2.22:
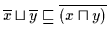 .
.
Umgekehrt ist
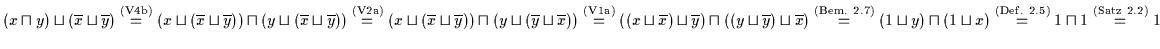 .
Daraus folgt nach Satz 2.22:
.
Daraus folgt nach Satz 2.22:
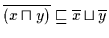 .
Nach (H2) folgt daher:
.
Nach (H2) folgt daher:
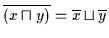 .
.
(b) Der Beweis verläuft dual.
Satz 2.24
Sei
 ein Boolescher Verband. Dann gilt für alle
ein Boolescher Verband. Dann gilt für alle 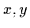 :
:
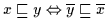
Beweis: ,, `` Es ist
`` Es ist
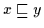 .
Dann gilt nach
Satz 2.22:
.
Dann gilt nach
Satz 2.22:
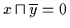 .
(V2b) liefert
.
(V2b) liefert
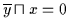 .
Daraus folgt wieder mit Satz 2.22:
.
Daraus folgt wieder mit Satz 2.22:
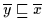 .
.
,,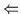 `` Es ist
`` Es ist
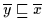 .
Dann gilt
nach Satz 2.22:
.
Dann gilt
nach Satz 2.22:
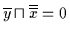 .
Dann
ist nach (V2b):
.
Dann
ist nach (V2b):
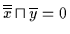 .
Gemäß
Satz 2.19 gilt dann:
.
Gemäß
Satz 2.19 gilt dann:
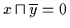 .
Dann gilt nach Satz
2.22:
.
Dann gilt nach Satz
2.22:
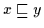 .
.
Satz 2.25
Sei
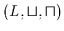 ein Boolescher Verband. Dann gilt für alle
ein Boolescher Verband. Dann gilt für alle 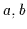 :
:
(a)
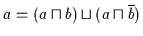
(b)
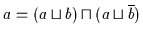
Beweis: (a) Es ist:
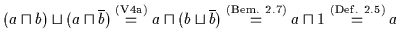 .
.
(b) Der Beweis ist dual.
Satz 2.26 (Transportationsregel von Peirce
)
Sei
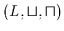 ein Boolescher Verband. Dann gilt für alle
ein Boolescher Verband. Dann gilt für alle 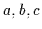 :
:
(a)
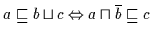
(b)
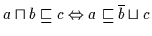
Beweis: (a) ,, `` Es gilt nach Voraussetzung
`` Es gilt nach Voraussetzung
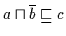 .
Nach Definition 2.10 gilt
.
Nach Definition 2.10 gilt
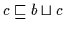 .
Mit (H3) folgt daher
.
Mit (H3) folgt daher
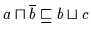 .
Andererseits gilt nach Definition 2.10
.
Andererseits gilt nach Definition 2.10
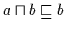 und
auch
und
auch
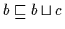 .
Daraus folgt nach (H3)
.
Daraus folgt nach (H3)
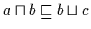 .
Nach Definition 2.10 folgt aus
.
Nach Definition 2.10 folgt aus
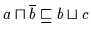 und
und
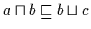 ,
daß
,
daß
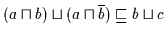 .
Dann gilt
nach Satz 2.25:
.
Dann gilt
nach Satz 2.25:
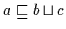 .
.
,,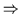 `` Es gilt nach Voraussetzung
`` Es gilt nach Voraussetzung
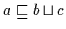 .
Nach Definition 2.10 gilt
.
Nach Definition 2.10 gilt
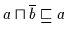 .
Mit (H3)
folgt daher
.
Mit (H3)
folgt daher
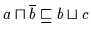 .
Andererseits gilt
nach Definition 2.10
.
Andererseits gilt
nach Definition 2.10
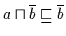 und auch
und auch
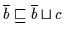 .
Daraus folgt nach
(H3)
.
Daraus folgt nach
(H3)
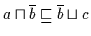 .
Nach Definition
2.10 folgt aus
.
Nach Definition
2.10 folgt aus
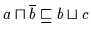 und
und
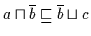 ,
daß
,
daß
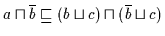 gilt.
Dann gilt nach Satz 2.25:
gilt.
Dann gilt nach Satz 2.25:
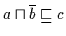 .
.
(b) ,, `` Den Beweis erhält man, indem man im Beweis (a)
,,
`` Den Beweis erhält man, indem man im Beweis (a)
,, `` jedes Auftreten von
`` jedes Auftreten von 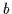 durch
durch 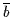 ersetzt und
umgekehrt.
ersetzt und
umgekehrt.
,, `` Den Beweis erhält man, indem man im Beweis (a)
,,
`` Den Beweis erhält man, indem man im Beweis (a)
,, `` jedes Auftreten von
`` jedes Auftreten von 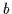 durch
durch 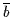 ersetzt und
umgekehrt.
ersetzt und
umgekehrt.
Definition 2.14 (Literal
)
Ein Literal ist die Variable für ein Objekt oder dessen Komplement aus dem
Trägerbereich eines Booleschen Verbandes.
Definition 2.15 (Boolesche Funktion)
Eine Boolesche Funktion ist ein beliebiger Ausdruck, der aus endlich vielen
Symbolen besteht, der die Verknüpfung von Konstanten und Variablen durch die
Operationen 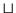 ,
,
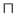 und
und  beschreibt.
Dabei werden ggf. Klammern zur Erzielung der Eindeutigkeit der Ausdrücke
eingesetzt.
beschreibt.
Dabei werden ggf. Klammern zur Erzielung der Eindeutigkeit der Ausdrücke
eingesetzt.
Bemerkung 2.9
Alle weiteren Ergebnisse dieses Abschnittes beziehen sich auf Boolesche
Verbände mit endlichem Trägerbereich, also auf endliche Boolesche Verbände.
Definition 2.16 (Minterm)
Sei 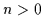 die Zahl der im Trägerbereich eines Booleschen Verbandes
vorkommenden verschiedenen Literale. Ein Minterm ist die Verknüpfung aller
die Zahl der im Trägerbereich eines Booleschen Verbandes
vorkommenden verschiedenen Literale. Ein Minterm ist die Verknüpfung aller 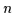 Literale durch die
Literale durch die 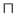 -Operation, wobei kein Literal doppelt vorkommt.
-Operation, wobei kein Literal doppelt vorkommt.
Satz 2.27
Mit 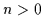 Variablen kann man
Variablen kann man 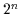 verschiedene Minterme erzeugen.
verschiedene Minterme erzeugen.
Beweis: (Vollständige Induktion) Sei 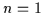 .
Dann gibt es nur eine
Variable, sie heiße
.
Dann gibt es nur eine
Variable, sie heiße 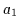 und zwei Minterme, nämlich
und zwei Minterme, nämlich 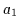 und
und
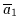 .
Die Behauptung gilt also für
.
Die Behauptung gilt also für 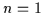 .
.
Angenommen die Behauptung gelte für 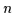 Variablen, es gebe also
Variablen, es gebe also 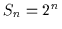 Minterme. Jeder dieser Minterme hat die Form
Minterme. Jeder dieser Minterme hat die Form
Fügt man eine weitere Variable 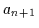 hinzu, so sehen die Minterme wie folgt
aus:
hinzu, so sehen die Minterme wie folgt
aus:
Dann gilt:
Der geklammerte Ausdruck ist einer der 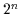 Minterme
Minterme 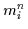 ,
also gilt:
,
also gilt:
d.h., jeder Minterm für 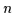 Variablen spaltet sich in zwei Minterme für
Variablen spaltet sich in zwei Minterme für 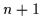 Variablen auf, nämlich in:
Variablen auf, nämlich in:
Insgesamt gibt es also
Minterme für 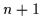 Variablen.
Variablen.
Definition 2.17 (kanonische Disjunktive Normalform
)
Eine Boolesche Funktion ist in kanonischer disjuktiver Normalform, wenn sie eine
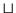 -Verknüpfung (Disjunktion) von Mintermen der Funktion ist, wobei kein
Minterm doppelt auftaucht.
-Verknüpfung (Disjunktion) von Mintermen der Funktion ist, wobei kein
Minterm doppelt auftaucht.
Die konstanten Funktionen 0 und 1 sind ebenfalls in kanonischer disjunktiver
Normalform für alle 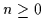 .
.
Satz 2.28
Die kanonische disjunktive Normalform, die bei 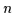 Variablen alle
Variablen alle 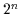 Minterme enthält, entspricht der 1.
Minterme enthält, entspricht der 1.
Beweis: Von den 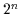 Mintermen enthalten
Mintermen enthalten 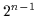 das Literal
das Literal 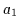 und
und 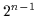 das Literal
das Literal
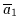 ,
wie bereits im Beweis von Satz
2.27 zu erkennen war. Aus den
,
wie bereits im Beweis von Satz
2.27 zu erkennen war. Aus den 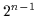 Mintermen, die das Literal
Mintermen, die das Literal
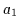 enthalten, wird
enthalten, wird 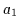 durch mehrfache Anwendung von (V4a)
,,ausgeklammert``. Ebenso wird mit dem Literal
durch mehrfache Anwendung von (V4a)
,,ausgeklammert``. Ebenso wird mit dem Literal
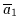 verfahren. Die
beiden jeweils verbleibenden Terme sind gemäß Beweis von Satz 2.27
identisch, wodurch sich die Disjunktion aller Minterme in der Form
verfahren. Die
beiden jeweils verbleibenden Terme sind gemäß Beweis von Satz 2.27
identisch, wodurch sich die Disjunktion aller Minterme in der Form
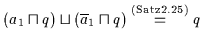 schreiben läßt, wobei
schreiben läßt, wobei  der identische Restterm ist.
der identische Restterm ist.
Wendet man nun auf  die gleiche Technik nocheinmal an, klammert jedoch
die gleiche Technik nocheinmal an, klammert jedoch
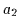 aus, so kann man
aus, so kann man 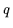 schreiben als
schreiben als
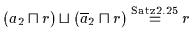 ,
wobei
,
wobei 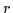 der verbleibende Restterm ist.
der verbleibende Restterm ist.
Anwendung dieser Technik bis zur Ausklammerung von 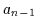 ergibt als Restterm
ergibt als Restterm
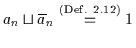 .
.
Satz 2.29
Jede Boolesche Funktion läßt sich in die kanonische disjunktive Normalform
umformen.
Beweis: Dieser Beweis wird durch die Angabe eines Konstruktionsverfahrens
geführt. Das Verfahren funktioniert wie folgt:
Sei 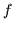 eine beliebige Boolesche Funktion von
eine beliebige Boolesche Funktion von 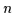 Variablen, einschließlich der
Konstanten 0 und 1. Wenn
Variablen, einschließlich der
Konstanten 0 und 1. Wenn 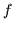 Ausdrücke der Form
Ausdrücke der Form
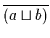 oder
oder
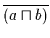 enthält, so ergibt die Anwendung von
Satz 2.23
enthält, so ergibt die Anwendung von
Satz 2.23
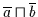 bzw.
bzw.
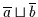 .
Das wiederholt man solange, bis jede
Komplement-Überstreichung nur noch über einer einzigen Variablen/Konstanten
steht. Gemäß Satz 2.19 werden doppelte Negationen aufgelöst. Durch
Anwendung von (V4a) und (V4b) erhält man Glieder, deren Literale nur durch
.
Das wiederholt man solange, bis jede
Komplement-Überstreichung nur noch über einer einzigen Variablen/Konstanten
steht. Gemäß Satz 2.19 werden doppelte Negationen aufgelöst. Durch
Anwendung von (V4a) und (V4b) erhält man Glieder, deren Literale nur durch
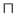 verbunden sind, und diese Glieder sind wiederum nur durch
verbunden sind, und diese Glieder sind wiederum nur durch 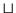 verknüpft. Enthält eines dieser Glieder eine 0, so ist gemäß Definition
2.5 das ganze Glied gleich 0 und kann daher gemäß Definition 2.5
ersatzlos entfallen, falls noch ein anderes Glied vorhanden ist. Ist das einzige
verbleibende Glied eine 0, so ist das Verfahren beendet. Enthält eines dieser
Glieder eine 1, so entfällt gemäß Definition 2.5 die 1, falls noch ein
anderes Literal in dem Glied vorkommt. Ist eines der Glieder gleich 1, so ist
gemäß Definition 2.5 die gesamte Disjunktion gleich 1 und das Verfahren
damit beendet. Angenommen ein Glied
verknüpft. Enthält eines dieser Glieder eine 0, so ist gemäß Definition
2.5 das ganze Glied gleich 0 und kann daher gemäß Definition 2.5
ersatzlos entfallen, falls noch ein anderes Glied vorhanden ist. Ist das einzige
verbleibende Glied eine 0, so ist das Verfahren beendet. Enthält eines dieser
Glieder eine 1, so entfällt gemäß Definition 2.5 die 1, falls noch ein
anderes Literal in dem Glied vorkommt. Ist eines der Glieder gleich 1, so ist
gemäß Definition 2.5 die gesamte Disjunktion gleich 1 und das Verfahren
damit beendet. Angenommen ein Glied 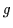 der Disjunktion enthält weder die
Variable
der Disjunktion enthält weder die
Variable 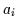 noch deren Komplement
noch deren Komplement
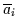 .
Dann ist
.
Dann ist
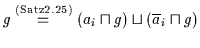 .
Wiederholt man diesen Schritt für jede fehlende
Variable in jedem Glied der Disjunktion, so erhält man schließlich eine
Disjunktion von Mintermen. Satz 2.2 erlaubt es, doppelt vorkommende
Glieder wegzulassen. Dann ist die entstandene Disjunktion von Mintermen eine
kanonische disjunktive Normalform.
.
Wiederholt man diesen Schritt für jede fehlende
Variable in jedem Glied der Disjunktion, so erhält man schließlich eine
Disjunktion von Mintermen. Satz 2.2 erlaubt es, doppelt vorkommende
Glieder wegzulassen. Dann ist die entstandene Disjunktion von Mintermen eine
kanonische disjunktive Normalform.
Da im beschriebenen Konstruktionsverfahren nur substituiert wird, also nur
Gleichungen verwendet werden, ist das Verfahren auch umkehrbar, d.h. Boolesche
Funktionen in kanonischer DNF teilen die Menge der Booleschen Funktionen in
Klassen äquivalenter Funktionen ein.
Satz 2.30
Bei 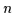 Variablen lassen sich genau
Variablen lassen sich genau 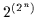 verschiedene disjunktive
Normalformen bilden.
verschiedene disjunktive
Normalformen bilden.
Beweis: Bei 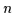 Variablen kann jeder der
Variablen kann jeder der 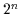 Minterme in einer
kanonischen disjunktiven Normalform vorkommen oder nicht, kann etwas zu der
Disjunktion beitragen oder nicht. Entsprechend der bekannten kombinatorischen
Grundregel zur Variation mit Wiederholung ergibt sich daher:
Minterme in einer
kanonischen disjunktiven Normalform vorkommen oder nicht, kann etwas zu der
Disjunktion beitragen oder nicht. Entsprechend der bekannten kombinatorischen
Grundregel zur Variation mit Wiederholung ergibt sich daher:
Ein andere Beweismöglichkeit beruht auf dem ,,Auswählen ohne Zurücklegen und
ohne Berücksichtigung der Reihenfolge``. Das entspricht der Art und Weise des
Auswählens der Minterme, denn erstens wird jeder Minterm nur einmal verwendet
und zweitens ist die Reihenfolge beliebig, da die Disjunktion kommutativ ist.
Für diesen Fall ist die Anzahl der Auswahlmöglichkeiten von 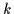 Objekten aus
einer Menge von
Objekten aus
einer Menge von 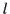 gleich
gleich
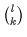 .
Für den Fall der Minterme, die die
kanonischen disjunktiven Normalformen bilden sollen, muß man die Auswahlen
aller
.
Für den Fall der Minterme, die die
kanonischen disjunktiven Normalformen bilden sollen, muß man die Auswahlen
aller
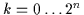 aus
aus 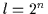 Mintermen betrachten. Dann ist die
Anzahl der verschiedenen kanonischen disjunktiven Normalformen gleich
Mintermen betrachten. Dann ist die
Anzahl der verschiedenen kanonischen disjunktiven Normalformen gleich
ein bekanntes Ergebnis der Kombinatorik. Dabei entspricht das Auftauchen keines
Mintermes der konstanten Funktion 0 und das Auftauchen aller Minterme gemäß
Satz 2.28 der konstanten Funktion 1.
Satz 2.31
Es gibt bei 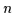 Variablen genau
Variablen genau 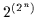 Äquivalenzklassen verschiedener
Boolescher Funktionen.
Äquivalenzklassen verschiedener
Boolescher Funktionen.
Beweis: Da jede Boolesche Funktion mit 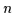 Variablen in eine Boolesche
Funktion in kanonisch disjunktiver Normalform mit
Variablen in eine Boolesche
Funktion in kanonisch disjunktiver Normalform mit 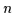 Variablen umgeformt werden
kann (Satz 2.29) und es für
Variablen umgeformt werden
kann (Satz 2.29) und es für 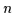 Variablen genau
Variablen genau 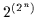 verschiedene kanonische disjunktive Normalformen gibt, heißt das, daß es genau
verschiedene kanonische disjunktive Normalformen gibt, heißt das, daß es genau
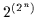 verschiedene Boolesche Funktionen für
verschiedene Boolesche Funktionen für 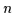 Variablen gibt.
Variablen gibt.


Nächste Seite: 2.2 Bemerkungen zum Hintergrundkalkül
Aufwärts: 2. Grundlagen
Vorherige Seite: 2. Grundlagen
Andreas Otte
1998-11-22
![]() als Variablen bezeichnet und dürfen sowohl überstrichen als auch indiziert
sein. Zusätzlich wird angenommen, daß ein Bereich mindestens ein Objekt
enthält.
als Variablen bezeichnet und dürfen sowohl überstrichen als auch indiziert
sein. Zusätzlich wird angenommen, daß ein Bereich mindestens ein Objekt
enthält.