- ... werden2.1
- Diese Art der Markierung wurde in [5]
eingeführt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
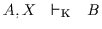 7.1
7.1
- Der Index K kann fehlen, wenn klar ist, um
welchen Kalkül es sich handelt, oder wenn von beliebigen Kalkülen die Rede
ist.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... werden7.2
- Damit ist verträglich, daß eine
minimale Lösung
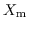 ,
aus der allein im allgemeinen Falle die
Konklusion nicht folgt, sich im besonderen als mit
,
aus der allein im allgemeinen Falle die
Konklusion nicht folgt, sich im besonderen als mit 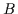 äquivalent erweist;
womit sich zugleich die Aufgabe stellt, notwendige und hinreichende Bedingungen
dafür anzugeben, daß dieser Fall eintritt.
äquivalent erweist;
womit sich zugleich die Aufgabe stellt, notwendige und hinreichende Bedingungen
dafür anzugeben, daß dieser Fall eintritt.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Fälle7.3
- Da man im Kalkül
BL
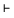 über Termnegation verfügt und daher alle syllogistischen
Relationen a, e, ..., ö ausdrücken kann, sind durch die Fälle 1 - 4
alle hier in Frage kommenden Möglichkeiten erschöpft.
über Termnegation verfügt und daher alle syllogistischen
Relationen a, e, ..., ö ausdrücken kann, sind durch die Fälle 1 - 4
alle hier in Frage kommenden Möglichkeiten erschöpft.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
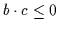 7.4
7.4
- Dies entspricht
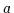 ë
ë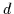 ,
,
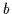 e
e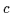 .
Da die Syllogistik im klassischen Sinne weder
.
Da die Syllogistik im klassischen Sinne weder 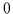 noch
noch 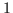 kennt, sollte man vielleicht lieber
kennt, sollte man vielleicht lieber
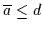 und
und
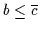 o.ä. schreiben. Wir bevorzugen i.a. die termnegationsfreie
Schreibweise oder eine solche, die den Zusammenhang von syllogistischer und
minimaler Lösung zu verdeutlichen geeignet erscheint.
o.ä. schreiben. Wir bevorzugen i.a. die termnegationsfreie
Schreibweise oder eine solche, die den Zusammenhang von syllogistischer und
minimaler Lösung zu verdeutlichen geeignet erscheint..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
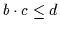 7.5
7.5
- Diese Lösung gilt auch schon für
distributive Verbände bzw. Begriffslogiken. Distributivität ist aber wohl
erforderlich, da man zum bequemen Nachweis der Lösungseigenschaft die sog. Schnittregel (vgl. [20]) zu benötigen scheint.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... geben7.6
- Abgesehen von der trivialen Lösung
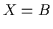 , hier also
, hier also
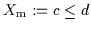 .
.
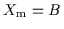 ist im Übrigen eine minimale Lösung für alle vier Fälle, hier allerdings
die einzig mögliche.
ist im Übrigen eine minimale Lösung für alle vier Fälle, hier allerdings
die einzig mögliche..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.