5. Minimaler Rückschluß im Kalkül BL$^{\vdash }$

Wir betrachten nun die vier möglichen Fälle¹¹, bei denen als bekannt genau eine Prämisse und eine Konklusion der Gestalt   $x \leq y$   oder   $x \not\leq y$¹²   auftreten. Die syllogistischen Lösungen ( $X_{\rm {s}}^{\rm {1}}$, $X_{\rm {s}}^{\rm {2}}$ etc.) und die minimalen ($X_{\rm {m}}$) besitzen dieselbe Gestalt und erfüllen die Bedingung, daß in $x$ und $y$ kein Beziehungszeichen, also $\leq$ oder $=$, enthalten ist, sofern dies nur für $a$, $b$, $c$, $d$ gilt.

1	aa	$a \leq b$, $X$  $\vdash$  $c \leq d$	$X_{\rm {s}}^{\rm {1}}$:	$c \leq a$, $b \leq d$
			$X_{\rm {s}}^{\rm {2}}$:	$1 \leq a + d$, $b \cdot c \leq 0$13
			$X_{\rm {m}}$:	$c \leq a + d$, $b \cdot c \leq d$14

2	ao	$a \leq b$, $X$  $\vdash$  $c \not\leq d$	$X_{\rm {s}}^{\rm {1}}$:	$a \not\leq d$, $b \leq c$
			$X_{\rm {s}}^{\rm {2}}$:	$a \cdot c \not\leq 0$, $b \cdot d \leq 0$
			$X_{\rm {s}}^{\rm {3}}$:	$1 \leq a + c$, $1 \not\leq b + d$
			$X_{\rm {s}}^{\rm {4}}$:	$d \leq a$, $c \not\leq b$
			$X_{\rm {m}}$:	$( a \cdot \overline{b} ) + ( c \cdot \overline{d} ) \not\leq 0$

3

oa

$a \not\leq b$, $X$  $\vdash$  $c \leq d$

Hier scheint es keine Lösung zu geben15 .

4	oo	$a \not\leq b$, $X$  $\vdash$  $c \not\leq d$	$X_{\rm {s}}^{\rm {1}}$:	$a \leq c$, $d \leq b$
			$X_{\rm {s}}^{\rm {2}}$:	$a \cdot d \leq 0$, $1 \leq b + c$
			$X^{*}$:	$a \leq b + c$, $a \cdot d \leq b$

.

5.1 Zur Begründung

Da sich unverneinte wie verneinte Subsumtionen   $a \leq b$   bzw.   $a \not\leq b$   jeweils in äquivalente Null-Subsumtionen    $a\overline{b} \leq 0$   bzw.    $a\overline{b} \not\leq 0$   umformen lassen¹⁶, reduzieren sich die Fälle 1 - 4 auf folgende (mit  $a\overline{b}$  für  $r$  und  $c\overline{d}$  für  $s$):

1'	$r \leq 0$  $\vdash$  $s \leq 0$	$X_{\rm {m}}$:	$s \leq r$
2'	$r \leq 0$  $\vdash$  $s \not\leq 0$	$X_{\rm {m}}$:	$r + s \leq 0$
3'	$r \not\leq 0$  $\vdash$  $s \leq 0$
4'	$r \not\leq 0$  $\vdash$  $s \not\leq 0$	$X^{*}$:	$r \leq s$

Ein Blick auf die zugehörigen Venn-Diagramme lehrt (Abb. 6 - 8a), daß die Lösungen 1', 2' und 4' Venn-minimal sind, wobei allerdings die Lösung 4' zuviel liefert:   $rs \not\leq 0$, an Stelle von   $s \not\leq 0$. Lösung 4' ist jedoch nicht minimal, da   $r \not\leq 0$, $s \not\leq 0$  $\vdash$  $r \leq s$   nicht gilt.

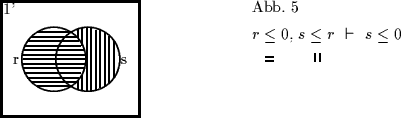
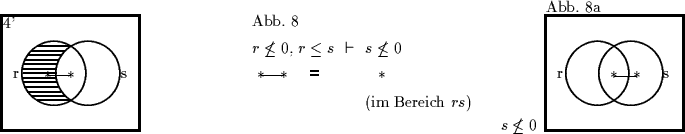
Die Minimalität der Lösungen für 1' und 2' sieht man so:

1':  Zu zeigen ist   $A$, $B$  $\vdash$  $X$; d.h.   $r \leq 0$, $s \leq 0$  $\vdash$  $s \leq r$.

Wegen des Axioms   $0 \leq r$   gilt aber schon   $s \leq 0$  $\vdash$  $s \leq r$, also   $B$  $\vdash$  $X$; also erst recht   $A$, $B$  $\vdash$  $X$.

2':  Auch hier gilt bereits   $B$  $\vdash$  $X$; d.h.    $s \not\leq 0$  $\vdash$   $r + s \not\leq 0$, wegen   $r + s \leq 0$, $s \leq r + s$  $\vdash$  $s \leq 0$   nach BL$^{\vdash }$-Theoremen¹⁹.

Zur Lösung des Falles 1 aa kann man - abgekürzt - auf folgendem Wege gelangen:

$a \leq b$, $X$  $\vdash$  $c \leq d$
$a\overline{b} \leq 0$, $X$  $\vdash$   $c\overline{d} \leq 0$	$X_{\rm {m}}$:	$c\overline{d} \leq a\overline{b}$                  nach 1' s.o.
	hieraus:	$c\overline{d} \leq a$, $c\overline{d} \leq \overline{b}$
		$c \leq a + d$, $bc \leq d$20

Jeweils nach bekannten Regeln der Booleschen Algebra.

Die Lösung des vierten Falles oo kann auf die des ersten aa zurückgeführt werden:

$a \not\leq b$, $X$  $\vdash$  $c \not\leq d$
$c \leq d$, $X$  $\vdash$  $a \leq b$

und weiter wie oben, oder aber

$a \not\leq b$, $X$  $\vdash$  $c \not\leq d$
$a \cdot \overline{b} \not\leq 0$, $X$  $\vdash$   $c \cdot \overline{d} \not\leq 0$
	$X^{*}$:    $a \cdot \overline{b} \leq c \cdot \overline{d}$	nach 4' s.o.

Auch der zweite Fall ao wird ähnlich behandelt:

$a \leq b$, $X$  $\vdash$  $c \not\leq d$
$a \cdot \overline{b} \leq 0$, $X$  $\vdash$   $c \cdot \overline{d} \not\leq 0$	$X_{\rm {m}}$:    $a \cdot \overline{b} + c \cdot \overline{d} \not\leq 0$	nach 2' s.o.

wobei man die Lösung 2' unmittelbar aus dem Venn-Diagramm oder aus der BL$^{\vdash }$-Regel (Satz)
  $r \leq 0$, $r + s \not\leq 0$  $\vdash$  $s \not\leq 0$²¹   entnehmen kann, die sich auf die Boolesche Regel   $r \leq 0$, $s \leq 0$  $\vdash$  $r + s \leq 0$   stützt.

Im übrigen kann man die Lösungen auch unmittelbar den Venn-Diagrammen für vier Begriffe entnehmen, z.B. im Falle aa:

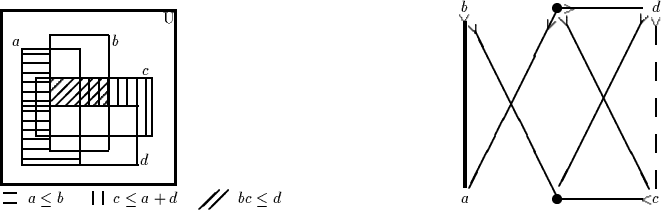
Mit dem Nebenergebnis, daß sich die minimale Lösung auch darstellen läßt als   $abc \leq d$, $bc \leq a + d$, $c \leq a + b + d$.