6. Teilminimalisierung

Wem aus irgendwelchen Gründen die jeweils minimale Lösung des Gesamtproblems   $A$, $X$  $\vdash$  $B$   nicht gefällt, der kann einen anderen Weg einschlagen, den wir ,,Teilminimalisierung`` nennen wollen.

Hierzu hat man sich mit Hilfe eines syllogistischen Lösungspaares einen Beweis herzustellen und dann bei jedem Beweisschritt die Minimallösung einzuführen; z.B. im Falle ao mit der ersten syllogistischen Lösung (siehe Abschnitt 5)   $a \leq b$, $a \not\leq d$, $b \leq c$  $\vdash$  $c \not\leq d$ :

Der Beweis

$$\infer{c \not\leq d}{\infer{a \leq c}{a \leq b & b \leq c} & a \not\leq d}$$

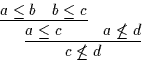
geht über in

$$\infer{c \not\leq d}{\infer{a \leq c}{a \leq b & ab \leq c}& a\overline{c} + c\overline{d} \not\leq 0}$$

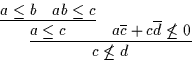
Als Lösung ergibt sich hier   $ab \leq c$, $a\overline{c} + c\overline{d} \not\leq 0$   im Gegensatz zur (Gesamt-)Minimallösung    $a\overline{b} + c\overline{d} \not\leq 0$. Sinngemäße Anwendung dieses Verfahrens auf die übrigen Fälle liefert eine Vielzahl von ,,teilweise`` minimalen Lösungen.

Gibt man die Einschränkung auf, daß die als Lösungen auftretenden positiven oder negativen Subsumtionen   $x \leq y$   bzw.   $x \not\leq y$   weder in x noch in y Beziehungszeichen, also  $\leq$  oder  $=$, enthalten dürfen, so besitzt jedes Rückschlußproblem   $A$, $X$  $\vdash$  $B$   die (triviale) Lösung:   $A \leq B$   wegen der Gültigkeit der BL$^{\vdash }$- Abtrennungsregel. In dem Kalkül der ,,gemischten Begriffslogik``²² BL $^{\vdash}_{\rm {u'}}$ läßt sich diese Lösung auch als minimal erweisen, weil hier unter bestimmten Bedingungen   $B$  $\vdash$  $A \leq B$   gilt.

Die Lösung   $A \leq B$   ist in BL $^{\vdash}_{\rm {u'}}$ mit den schon bekannten Minimallösungen jeweils äquivalent relativ zu $A$, d.h. es gilt:

$A$, $A \leq B$  $\vdash$  $X_{\rm {m}}$   und   $A$, $X_{\rm {m}}$  $\vdash$  $A \leq B$; z.B. im Falle aa:

$a \leq b$, $( a \leq b ) \leq ( c \leq d )$  $\vdash$   $c\overline{d} \leq a\overline{b}$     sowie

$a \leq b$, $c\overline{d} \leq a\overline{b}$  $\vdash$   $( a \leq b ) \leq ( c \leq d )$;

wie überhaupt zwei verschiedene minimale Lösungen relativ zu $A$ stets äquivalent sind²³.

Wollte man das Rückschlußproblem in der (vollen) Urteilslogik, etwa im Kalkül BL $^{\vdash}_{\rm {u}}$ studieren, so wäre es sinnvoll, beliebige Ausdrücke, etwa auch solche der Gestalt   $U+V$,    $\prod_{\rm {i}}{A_{\rm {i}}}$   etc. zuzulassen²⁴.