4. Minimalitätsbedingungen

Zur Einführung diene ein Beispiel aus der Syllogistik, dem der Modus Barbara zugrundeliegt⁷:

Alle $a$ sind $b$,	$X$	$\vdash$	Alle $a$ sind $c$
$a$a$b$,	$X$	$\vdash$	$a$a$c$
$a \leq b$,	$X$	$\vdash$	$a \leq c$

Hier lautet die syllogistische Lösung $X_{\rm {syll}}$ nach v. Freytag Löringhoff:

$$X_{\rm {syll}}: ~~b \leq c$$

Ersichtlich gilt:   $a \leq b$, $b \leq c$  $\vdash$  $a \leq c$. Aber ist diese Lösung irgendwie minimal?

Im Vennschen Umfangsdiagramm⁸ (s. Abb. 1) sieht das so aus:

Aus dem Diagramm entnimmt man ohne weiteres, daß die syllogistische Lösung sozusagen zu viel liefert. Um aus   $a \leq b$    $a \leq c$   zu gewinnen, genügt folgende Schraffierung (siehe Abb. 2):

Die Lösung   $ab \leq c$   ist - wie auch aus dem Diagramm unmittelbar ersichtlich - echt schwächer als die syllogistische, denn aus   $b \leq c$   folgt   $ab \leq c$, aber nicht umgekehrt.

Im anschaulichen, durch das Venn-Diagramm gegebenen Sinne ist sie auch am schwächsten, denn für den Fall, daß   $ab \leq c$   nicht, also    $ab \not\leq c$   gilt, ist   $a \leq c$   aus   $a \leq b$   nicht zu beweisen (siehe Abb. 3).

Dies gilt nicht für die syllogistische Lösung   $b \leq c$  , was man sich ebenfalls leicht am Venn-Diagramm klar macht. Denn angenommen,   $b \leq c$   gelte nicht, also   $b \not\leq c$, so ist diese Lage immer noch mit   $ab \leq c$  (siehe Abb. 2) verträglich (siehe Abb. 4):

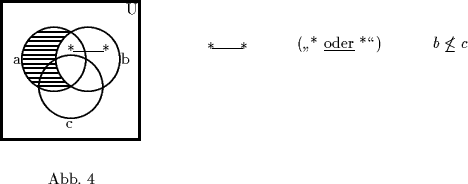
Als ,,V(enn)-minimal`` wollen wir im folgenden eine Lösung des Rückschlußproblems bezeichnen, die sich durch Betrachtung eines zugehörigen Venn-Diagramms als zur Gewinnung der Konklusion unerläßlich erweist.

Eine andere Möglichkeit bestünde darin, ,,minimal (schlechthin)`` eine Lösung zu nennen, die relativ zum bekannten Prämissensystem  $A$  bzgl. der Ableitbarkeitsbeziehung ,,$\vdash$`` schwächer ist als alle anderen Lösungen.

Wir definieren daher folgendermaßen (mit einem Nachtrag den Begriff ,,Lösung`` betreffend):

a)

,,$X$ ist Lösung des Rückschlußproblems (relativ zu  $A$, $B$  und zum Kalkül K)``, genau wenn gilt:
$A$, $X$   $\vdash_{\rm K}$  $B$.

(,,$B$ ist aus  $A$  und  $X$  im Kalkül K beweisbar``)

b)

,,$X$ ist  minimal``, genau wenn gilt:

Für alle $Y$: Wenn   $A$, $Y$   $\vdash_{\rm {K}}$  $B$, dann   $A$, $Y$   $\vdash_{\rm {K}}$  $A$, $X$.

(,, Alle Lösungen  $Y$  haben zusammen mit  $A$  im Kalkül K  $A$  und  $X$  zur Folge``)

Diese Bedingung ist - wie sich leicht zeigen läßt⁹ - äquivalent mit der einfacheren:   $A$, $B$   $\vdash_{\rm {K}}$  $X$, die wir daher im folgenden benutzen werden, so daß sich aus  a) und b)  ergibt:

,,$X$ ist minimale Lösung des Rückschlußproblems (relativ zu  $A$, $B$, K)``, genau wenn gilt:   $A$, $X$   $\vdash_{\rm {K}}$  $B$   und   $A$, $B$   $\vdash_{\rm {K}}$  $X$¹⁰.