Die Begriffslogik hat ihre Wurzeln in der Philosophie. Als ihr geistiger Vater muß der griechische Philosoph Aristoteles angesehen werden. Im Mittelalter beschäftigte man sich ausgiebig mit Randproblemen und erst seit kurzer Zeit gibt es brauchbare Formalisierungen.
Zunächst wird eine formale Sprache der Begriffslogik eingeführt:
| Grundzeichen | a b c ... | Variablen | |
| A B C ... | |||
| 0 1 | Konstanten | ||
| Beziehungszeichen | |||
| |
Verknüpfungszeichen |
| Ausdrücke | Terme |
| 1. Zeichen des Alphabetes (Variablen und Konstanten), die auch (mehrfach) mit Indizes oder Exponenten (aus dem Alphabet) versehen sein dürfen. | |
| 2. Sind |
| Formeln | |
| 1. Zeichen des Alphabetes, die auch (mehrfach) mit Indizes oder Exponenten (aus dem Alphabet) versehen sein dürfen. | |
| 2. Sind |
|
| 3. Sind |
Insbesondere gilt hierdurch, daß in der Begriffslogik z.B. Ausdrücke der Form
![]() erlaubt sind.
erlaubt sind. ![]() und = werden dadurch
praktisch auch zu Verknüpfungszeichen. Die eindeutige Lesbarkeit der Ausdrücke
wird nötigenfalls durch Setzen von Klammern gewährleistet.
und = werden dadurch
praktisch auch zu Verknüpfungszeichen. Die eindeutige Lesbarkeit der Ausdrücke
wird nötigenfalls durch Setzen von Klammern gewährleistet.
Es gelten die folgenden Axiome ( Grundformeln und Grundregeln ):
| A1 | A6 |
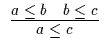 |
| A2a |
|
A7 |
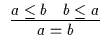 |
|||||
| A2b |
|
| A3a | A8a |
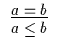 |
A8b |
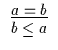 |
|||
| A3b |
| A4a | A9 |
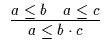 |
||||||
| A4b |
| A5a |
|
A10 |
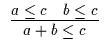 |
|||||
| A5b |
|
Der waagerechte Strich in den Grundregeln zeigt einen Ableitungsschritt an, oberhalb des Striches stehen die Prämissen, unterhalb die Konklusion. Damit liegt ein formales System der Begriffslogik vor. Dieses System werden wir mit BL bezeichnen. Man könnte viele Sätze mit diesem Axiomensystem beweisen, ohne zu wissen, was überhaupt ein ,,Begriff`` ist.
Man kann die Logik als allgemeine Lehre vom Argumentieren, Begründen, Beweisen, kurz als Lehre vom Schließen auffassen. Schlüsse als Gegenstände der Logik bauen sich aus Urteilen (Prämissen, Konklusionen) auf, und diese wiederum bestehen unter anderem aus Begriffen. Begriffslogik hat mit den Beziehungen und Verknüpfungen von Begriffen zu tun. Mit einem Begriff kann alles repräsentiert werden, was gemeint werden kann, also Existierendes wie Nichtexistierendes, Widerspruchsvolles wie Widerspruchsfreies, Wahres wie Unwahres, Denkbares wie Undenkbares, usw.
Die in der obigen Axiomatik eingeführte Beziehung ![]() zwischen zwei
Begriffen wollen wir als Art-Gattungs-Beziehung bezeichnen. Dabei ist
zwischen zwei
Begriffen wollen wir als Art-Gattungs-Beziehung bezeichnen. Dabei ist ![]() in
der Beziehung
in
der Beziehung ![]() die Art und
die Art und ![]() die Gattung. Der Begriff ,,Hund`` etwa
ist Art des Gattungsbegriffes ,,Lebewesen``.
die Gattung. Der Begriff ,,Hund`` etwa
ist Art des Gattungsbegriffes ,,Lebewesen``.
Vom Inhalt eines Begriffes kann gesagt werden, daß er mindestens den Inhalt seiner Gattungen enthält, und höchstens den Inhalt seiner Arten.
Vom Umfang eines Begriffes kann gesagt werden, daß er mindestens den Umfang seiner Arten enthält, und höchstens den Umfang seiner Gattungen.
Der Inhalt eines Begriffes beschreibt die Merkmale des Begriffes, sein Umfang den Anwendungsbereich des Begriffes. Eine Art hat also mindestens soviel Inhalt wie ihre Gattung. Die Art kann aber auch mehr Inhalt haben als ihre Gattung. Je spezifischer ein Begriff wird, desto geringer wird dabei natürlich sein Umfang, also daß, worauf er zutrifft. Das ist die sogenannte Inhalts-Umfangs-Relation, je mehr Inhalt, desto weniger Umfang, und umgedreht.
Auf diese Weise entsteht eine Art Begriffsgerüst, welches die
Art-Gattungsbeziehungen zwischen Begriffen darstellt. Früher nannte man dieses
Gerüst die ,,Begriffspyramide``, eine so ebenmäßige Form hat es allerdings
nicht, lediglich die grobe Orientierung stimmt. Ausgehend von einer breiten
Basis sehr spezieller Begriffe verjüngt sich das Gerüst zu immer allgemeineren
Begriffen, bis hin zum Begriff des ,,Meinbaren``, der an der Spitze steht, denn
alles ist meinbar. Der Begriff ,,Meinbar`` ist sozusagen der inhaltsleerste
Begriff. Das ist auch in der Axiomatik erkennbar, denn es gilt ![]() .
Der
Begriff des ,,Nicht-Meinbaren`` ist dagegen widersprüchlich, gibt man ihn an,
so hat man ihn bereits gemeint. Ein widersprüchlicher Begriff ist sozusagen der
umfangsleerste Begriff, nur er selbst ist in seinem Umfang. Das wird in der
Axiomatik durch
.
Der
Begriff des ,,Nicht-Meinbaren`` ist dagegen widersprüchlich, gibt man ihn an,
so hat man ihn bereits gemeint. Ein widersprüchlicher Begriff ist sozusagen der
umfangsleerste Begriff, nur er selbst ist in seinem Umfang. Das wird in der
Axiomatik durch ![]() ausgedrückt, wodurch auch klar wird, daß es nur
einen widersprüchlichen Begriff gibt, unbeschadet seiner vielen
Erscheinungsformen.
ausgedrückt, wodurch auch klar wird, daß es nur
einen widersprüchlichen Begriff gibt, unbeschadet seiner vielen
Erscheinungsformen.
Die Art-Gattungsbeziehung zwischen den Begriffen ![]() und
und ![]() kennzeichnet aber
auch das Urteil ,,Alle
kennzeichnet aber
auch das Urteil ,,Alle ![]() sind
sind ![]() ``. Die bekannten vier aristotelischen
Urteilsformen, welche die Bausteine der sogenannten Syllogistik (ein von
Aristoteles begründeter Teil der Begriffslogik) bilden,
``. Die bekannten vier aristotelischen
Urteilsformen, welche die Bausteine der sogenannten Syllogistik (ein von
Aristoteles begründeter Teil der Begriffslogik) bilden,
lassen sich bisher aber nur teilweise mit der oben beschrieben Axiomatik
erfassen. Sie ist noch nicht ausreichend zur Darstellung der klassischen Logik
und wird später erweitert werden. Immerhin genügt sie aber zur Darstellung des
a- wie des e-Urteils und den zugehörigen Schlüssen. Das a-Urteil entspricht
der Art-Gattungsbeziehung, also der Form ![]() .
Auch das e-Urteil ,,Kein A
ist B`` oder auch ,,Alle A sind nicht-B`` kann als eine Art-Gattungsbeziehung
verstanden werden, nämlich als
.
Auch das e-Urteil ,,Kein A
ist B`` oder auch ,,Alle A sind nicht-B`` kann als eine Art-Gattungsbeziehung
verstanden werden, nämlich als
![]() oder auch als
oder auch als
![]() .
.
Die Axiome des oben beschriebenen Systems sind vor diesem Hintergrund wie folgt zu verstehen:
Andererseits kann man den Begriff ,,a`` auch beschreiben als Und-Verknüpfung der ,,a oder b`` mit den ,,a oder Nicht-b,,.
Aufgrund des sehr weit gefaßten Begriffes vom Begriff sind auch Urteile,
da meinbar, durch Begriffe repräsentierbar. Dazu dienten auch die besonderen
Definitionen in der formalen Sprache. Die Axiomatik enthält aber keine
speziellen Regeln zur Behandlung dieser Beziehungsbegriffe. Wir werden daher
diese Möglichkeit, die die Begriffslogik bietet, ja, die geradezu die Logik
ausmacht, zunächst nicht nutzen, und BL typisch verbandstheoretisch, also
lediglich wie den Kalkül BV
![]() interpretieren. Diesen, in seiner
formalen Sprache reduzierten Kalkül wollen wir BV
interpretieren. Diesen, in seiner
formalen Sprache reduzierten Kalkül wollen wir BV![]() nennen.
nennen.
Das aristotelische i- und o-Urteil lassen sich mit der obigen Axiomatik für BL zunächst nicht erfassen, denn das o-Urteil ist die Negation des a-Urteils und das i-Urteil ist die Negation des e-Urteils. Für die Negation von Urteilen gibt es in BL keine Axiome.
Diese vorgelegte Axiomatik zielt aber zunächst nur auf die Beziehung ,,Begriffslogik - Boolescher Verband``, in einer Erweiterung wird die Behandlung der restlichen Urteile ebenfalls möglich sein.
Andererseits zeigte die Betrachtung der Venn-Diagramme, daß es noch weitere
Unterordungen gibt, die in dieser Form nicht so einfach, d.h. ohne negierte
Begriffe und einheitliche Begriffsfolge, von den aristotelischen Urteilsformen
abgedeckt werden, nämlich
![]() und
und
![]() ,
bzw. deren Negationen. In neuerer Zeit wurde daher die
aristotelische Urteilssystematik erweitert, z.B. in [6]:
,
bzw. deren Negationen. In neuerer Zeit wurde daher die
aristotelische Urteilssystematik erweitert, z.B. in [6]:
ä- und ö-Urteil sind dabei noch gut zu fassen, denn sie lassen sich relativ einfach in a- bzw. o-Urteile umformen. Das ë-Urteil drückt dagegen aus, daß die Begriffe A und B keinen gemeinsamen Inhalt haben ( mit der Ausnahme, daß beide meinbar sind ), was man mit einer nahezu totalen Unähnlichkeit übersetzen könnte. Das ï-Urteil bedeutet dagegen, daß die Begriffe A und B über die Meinbarkeit hinaus gemeinsamen Inhalt haben, sich also in einem abstrakten Sinne ähnlich sind.
Nun werden einige später nützliche Hilfssätze bewiesen. Diese Beweise liegen sämtlich in der sogenannten Baumform vor. Die Baumform ist wie folgt definiert: An der Wurzel liegt die Konklusion, an den Blättern die Prämissen oder aber Grundformeln. Dazwischen sind einzelne Ableitungschritte von den Blättern zu der Wurzel hin durch einen waagerechten Strich gekennzeichnet, der die Anwendung einer Grundregel oder aber einer abgeleiteten ( vorher bewiesenen ) Regel anzeigt. Dabei ist die Reihenfolge der Prämissen unerheblich, ebenso ist eine beliebige Vervielfachung der Prämissen und Grundformeln möglich. Diese Darstellungsform erlaubt eine sehr anschauliche Darlegung der einzelnen Beweisschritte.
Um auch in der linearen Darstellung einen Ableitungszusammenhang kennzeichen zu
können, wird das Zeichen ![]() eingeführt, wobei
eingeführt, wobei ![]() bedeutet,
daß aus
bedeutet,
daß aus ![]()
![]() abgeleitet werden kann.
abgeleitet werden kann. ![]() kennzeichnet dementsprechend
einen Ableitungszusammenhang in der umgedrehten Richtung.
kennzeichnet dementsprechend
einen Ableitungszusammenhang in der umgedrehten Richtung.
Beweis:
(a)
![\begin{displaymath}
\infer
[A6]
{a \cdot \overline{b} \leq c}
{\infer
[A9]
...
...ce
[A5]
{( c + b ) \cdot ( c + \overline{b} ) \leq c}
{}
}
\end{displaymath}](img493.gif)
![\begin{displaymath}
\infer
[A6]
{a \leq b + c}
{\deduce
[A5]
{a \leq ( a \c...
...rline{b} \leq c
&
\deduce
[A3]
{c \leq b + c}
{}
}
}
}
\end{displaymath}](img494.gif)
(b)
![\begin{displaymath}
\infer
[A6]
{a \cdot b \leq c}
{\infer
[A9]
{a \cdot b ...
...ce
[A5]
{( c + b ) \cdot ( c + \overline{b} ) \leq c}
{}
}
\end{displaymath}](img495.gif)
![\begin{displaymath}
\infer
[A6]
{a \leq \overline{b} + c}
{\deduce
[A5]
{a ...
...educe
[A3]
{\overline{b} \leq \overline{b} + c}
{}
}
}
}
\end{displaymath}](img496.gif)
Beweis:
(a)
![\begin{displaymath}
\infer
[A7]
{a + 0 = a}
{\infer
[A10]
{a + 0 \leq a}
{...
...4]
{0 \leq a}
{}
}
&
\deduce
[A3]
{a \leq a + 0}
{}
}
\end{displaymath}](img501.gif)
(b)
![\begin{displaymath}
\infer
[A7]
{a \cdot 0 = 0}
{\deduce
[A2]
{a \cdot 0 \leq 0}
{}
&
\deduce
[A4]
{0 \leq a \cdot 0}
{}
}
\end{displaymath}](img502.gif)
(c)
![\begin{displaymath}
\infer
[A7]
{a \cdot 1 = a}
{\infer
[A9]
{a \leq a \cdo...
...{a \leq 1}
{}
}
&
\deduce
[A2]
{a \cdot 1 \leq a}
{}
}
\end{displaymath}](img503.gif)
(d)
![\begin{displaymath}
\infer
[A7]
{a + 1 = 1}
{\deduce
[A4]
{a + 1 \leq 1}
{}
&
\deduce
[A3]
{1 \leq a + 1}
{}
}
\end{displaymath}](img504.gif)
Beweis:
(a)
![\begin{displaymath}
% latex2html id marker 5058\infer
[Satz\ \ref{SATZ29}]
{...
... b + 0}
{a \leq b
&
\deduce
[A3]
{b \leq b + 0}
{}
}
}
\end{displaymath}](img509.gif)
![\begin{displaymath}
% latex2html id marker 5059\infer
[A6]
{a \leq b}
{\inf...
...leq b}
{\deduce
[Satz\ \ref{SATZ29b}]
{b + 0 = 0}
{}
}
}
\end{displaymath}](img510.gif)
(b)
![\begin{displaymath}
% latex2html id marker 5060\infer
[Satz\ \ref{SATZ29}]
{...
... \deduce
[A3]
{\overline{b} \leq \overline{b} + 0}
{}
}
}
\end{displaymath}](img511.gif)
![\begin{displaymath}
% latex2html id marker 5061\infer
[A6]
{a \leq \overline...
...educe
[Satz\ \ref{SATZ29b}]
{\overline{b} + 0 = 0}
{}
}
}
\end{displaymath}](img512.gif)
(c)
![\begin{displaymath}
% latex2html id marker 5062\infer
[Satz\ \ref{SATZ29}]
{...
... b}
{\deduce
[A2]
{1 \cdot a \leq a}
{}
&
a \leq b
}
}
\end{displaymath}](img513.gif)
![\begin{displaymath}
% latex2html id marker 5063\infer
[A6]
{a \leq b}
{\inf...
...{SATZ29}]
{1 \cdot a \leq b}
{1 \leq \overline{a} + b}
}
}
\end{displaymath}](img514.gif)
(d)
![\begin{displaymath}
% latex2html id marker 5064\infer
[Satz\ \ref{SATZ29}]
{...
...erline{a} \leq \overline{a}}
{}
&
\overline{a} \leq b
}
}
\end{displaymath}](img515.gif)
![\begin{displaymath}
% latex2html id marker 5065\infer
[A6]
{\overline{a} \le...
...{SATZ29}]
{1 \cdot \overline{a} \leq b}
{1 \leq a + b}
}
}
\end{displaymath}](img516.gif)
Beweis:
(a)
![\begin{displaymath}
% latex2html id marker 5066\infer
[Satz\ \ref{SATZ30}]
{...
...ot \overline{a} \leq 0}
{\deduce
[A3]
{a \leq a + 0}
{}
}
\end{displaymath}](img519.gif)
(b)
![\begin{displaymath}
% latex2html id marker 5067\infer
[Satz\ \ref{SATZ30}]
{...
...q a + \overline{a}}
{\deduce
[A2]
{1 \cdot a \leq a}
{}
}
\end{displaymath}](img520.gif)
Beweis:
![\begin{displaymath}
% latex2html id marker 5068\infer
[A7]
{a = \overline{\o...
...leq \overline{a} + a}
{\deduce
[A1]
{a \leq a}
{}
}
}
}
\end{displaymath}](img522.gif)
Beweis:
(a)
![\begin{displaymath}
\infer
[A7]
{a + b = b + a}
{\infer
[A10]
{a + b \leq b...
...{b \leq a + b}
{}
&
\deduce
[A3]
{a \leq a + b}
{}
}
}
\end{displaymath}](img525.gif)
(b)
![\begin{displaymath}
\infer
[A7]
{a \cdot b = b \cdot a}
{\infer
[A9]
{a \cd...
... a \leq a}
{}
&
\deduce
[A2]
{b \cdot a \leq b}
{}
}
}
\end{displaymath}](img526.gif)
Beweis:
![\begin{displaymath}
\infer
[A9]
{\rule[-2mm]{0mm}{4mm}a \cdot b \cdot c \leq a...
...cdot c}
{}
&
\deduce
[A2]
{b \cdot c \leq b}
{}
}
}
}
\end{displaymath}](img528.gif)
![\begin{displaymath}
\infer
[A9]
{\rule[-2mm]{0mm}{4mm}a \cdot c \cdot b \leq a...
...cdot b}
{}
&
\deduce
[A2]
{c \cdot b \leq c}
{}
}
}
}
\end{displaymath}](img529.gif)
Beweis:
![\begin{displaymath}
% latex2html id marker 5073\infer
[Satz\ \ref{SATZ30}({\r...
...30}({\rm a})]
{a \cdot \overline{b} \leq 0}
{a \leq b}
}
}
\end{displaymath}](img531.gif)
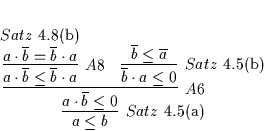
Beweis:
(a)
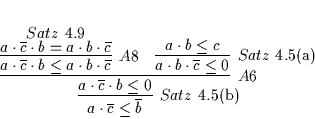
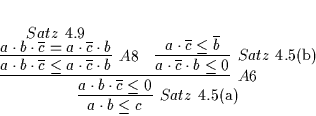
(b)
![\begin{displaymath}
% latex2html id marker 5077\infer
[A6]
{\overline{c} \le...
...1a}({\rm a})]
{\overline{a} + b \leq b + \overline{a}}
{}
}
\end{displaymath}](img537.gif)
![\begin{displaymath}
% latex2html id marker 5078\infer
[A6]
{a \leq b + c}
{...
...uce
[Satz\ \ref{SATZ31a}({\rm a})]
{c + b \leq b + c}
{}
}
\end{displaymath}](img538.gif)
Beweis:
(a)
![\begin{displaymath}
% latex2html id marker 5079\infer
[A9]
{\overline{a + b}...
...} \leq \overline{b}}
{\deduce
[A3]
{b \leq a + b}
{}
}
}
\end{displaymath}](img541.gif)
![\begin{displaymath}
% latex2html id marker 5080\infer
[A6]
{\overline{a} \cd...
...ne{a} \cdot \overline{b} \leq \overline{b}}
{}
}
}
}
}
}
\end{displaymath}](img542.gif)
(b)
![\begin{displaymath}
% latex2html id marker 5081\infer
[A6]
{\overline{a \cdo...
...e{a} + \overline{b}}} = \overline{a} +
\overline{b}}
{}
}
}
\end{displaymath}](img543.gif)
![\begin{displaymath}
% latex2html id marker 5082\infer
[A10]
{\overline{a} + ...
...line{a \cdot b}}
{\deduce
[A2]
{a \cdot b \leq b}
{}
}
}
\end{displaymath}](img544.gif)
Die vorgelegte begriffslogische Axiomatik ist ein Boolescher Verband, wenn man
![]() mit
mit ![]() übersetzt, sowie
übersetzt, sowie ![]() mit
mit ![]() ,
,
![]() mit
mit
![]() ,
0 mit 0, 1 mit 1 und
,
0 mit 0, 1 mit 1 und ![]() mit
mit
![]() .
.
Beweis: Es ist nachzuweisen, daß sich alle Axiome des Booleschen Verbandes aus den Axiomen der Begriffslogik nach Übersetzung ableiten lassen.
(V1a)
![\begin{displaymath}
\infer
[A10]
{a + ( b + c ) \leq ( a + b ) + c }
{\infer
...
... c}
{}
}
&
\deduce
[A3]
{c \leq ( a + b ) + c}
{}
}
}
\end{displaymath}](img546.gif)
![\begin{displaymath}
\infer
[A10]
{( a + b ) + c \leq a + ( b + c ) }
{\infer
...
...c}
{}
&
\deduce
[A3]
{b + c \leq a + ( b + c )}
{}
}
}
\end{displaymath}](img547.gif)
(V1b)
![\begin{displaymath}
\infer
[A9]
{a \cdot ( b \cdot c ) \leq ( a \cdot b ) \cdo...
...b \cdot c}
{}
&
\deduce
[A2]
{b \cdot c \leq c}
{}
}
}
\end{displaymath}](img548.gif)
![\begin{displaymath}
\infer
[A9]
{( a \cdot b ) \cdot c \leq a \cdot ( b \cdot ...
... }
&
\deduce
[A2]
{( a \cdot b ) \cdot c \leq c}
{}
}
}
\end{displaymath}](img549.gif)
(V2a)
Bereits durch Satz 4.8 bewiesen.
(V2b)
Bereits durch Satz 4.8 bewiesen.
(V3a)
![\begin{displaymath}
\infer
[A7]
{a = a \cdot ( a + b )}
{\deduce
[A2]
{a \c...
...1]
{a \leq a}
{}
&
\deduce
[A3]
{a \leq a + b}
{}
}
}
\end{displaymath}](img550.gif)
(V3b)
![\begin{displaymath}
\infer
[A7]
{a = a + ( a \cdot b )}
{\infer
[A10]
{a + ...
...a}
{}
}
&
\deduce
[A3]
{a \leq a + ( a \cdot b )}
{}
}
\end{displaymath}](img551.gif)
(V4a)
![\begin{displaymath}
% latex2html id marker 5089\infer
[Satz\ \ref{SATZ31d}]
...
...verline{b} \cdot \overline{c} = \overline{b + c}}
{}
}
}
}
\end{displaymath}](img552.gif)
![\begin{displaymath}
\infer
[A9]
{( a \cdot b ) + ( a \cdot c ) \leq a \cdot ( ...
...t c \leq c}
{}
&
\deduce
[A3]
{c \leq b + c}
{}
}
}
}
\end{displaymath}](img553.gif)
(V4b)
![\begin{displaymath}
\infer
[A10]
{a + ( b \cdot c ) \leq ( a + b ) \cdot ( a +...
...t c \leq c}
{}
&
\deduce
[A3]
{c \leq a + c}
{}
}
}
}
\end{displaymath}](img554.gif)
![\begin{displaymath}
% latex2html id marker 5092\infer
[Satz\ \ref{SATZ31d}]
...
...
[A2]
{( a + b ) \cdot ( a + c ) \leq a + c}
{}
}
}
}
}
\end{displaymath}](img555.gif)
Die begriffslogische 0 ist ein Nullobjekt eines Verbandes, denn sie erfüllt nach Übersetzung gemäß Satz 4.4 dessen Definition.
Die begriffslogische 1 ist ein Einsobjekt eines Verbandes, denn sie erfüllt nach Übersetzung gemäß Satz 4.4 dessen Definition.
Die eindeutige begriffslogische Negatoperation erfüllt mit Satz 4.6 die Komplement-Definition der Verbandstheorie.
Auch hier muß wieder die Substitutionsregel des Booleschen Gleichungskalküls
bewiesen werden. Der Beweis ist jedoch (nach Übersetzung) identisch mit dem
Beweis aus Satz 4.1, deshalb soll er hier entfallen. Das gilt
allerdings nur für den Kalkül BV![]() ,
nicht für BL, denn dann müßte
die Substitutionsregel auch noch für die ,,Verknüpfungszeichen`` ,,
,
nicht für BL, denn dann müßte
die Substitutionsregel auch noch für die ,,Verknüpfungszeichen`` ,,![]() ``
bzw. ,,=`` bewiesen werden, wofür die vorgelegte Axiomatik aber keine
Möglichkeiten bietet.
``
bzw. ,,=`` bewiesen werden, wofür die vorgelegte Axiomatik aber keine
Möglichkeiten bietet.
Ein Boolescher Verband ist eine Begriffslogik, wenn man ![]() mit
mit ![]() übersetzt, sowie
übersetzt, sowie ![]() mit
mit ![]() ,
,
![]() mit
mit ![]() ,
0 mit 0, 1 mit 1 und
,
0 mit 0, 1 mit 1 und
![]() mit
mit ![]() .
.
Beweis: Es ist nachzuweisen, daß sich alle Axiome der Begriffslogik aus den Axiomen des Booleschen Verbandes nach Übersetzung ableiten lassen.
Grundformel (A1) entspricht nach Übersetzung Axiom (H1).
Die Grundformeln in (A2) und (A3) sind nach Übersetzung durch Definition 2.9 abgedeckt.
Die Grundformeln in (A4) sind nach Übersetzung durch Definition 2.8 abgedeckt.
Die Grundformeln in (A5) sind nach Übersetzung durch Satz 2.25 bewiesen.
Die Grundregel (A6) entspricht nach Übersetzung Axiom (H3).
Die Grundregel (A7) ist nach Übersetzung durch Satz 2.16 bewiesen.
Die Grundregeln in (A8) sind nach Übersetzung durch Satz 2.16 bewiesen.
Die Grundregeln in (A9) und (A10) sind nach Übersetzung durch Satz 2.10 bewiesen.
Die Beziehung ![]() (auch Unterordnung genannt) ist also eine Halbordnung im
Sinne des Booleschen Halbordnungskalküls (H1-H6).
(auch Unterordnung genannt) ist also eine Halbordnung im
Sinne des Booleschen Halbordnungskalküls (H1-H6).
Es hat sich aber auch gezeigt, daß die Axiome (H4) und (H6) durch die schwächeren Axiome A5a und A5b ersetzt werden können und trotzdem noch die Distributivität gewährleistet bleibt. Diese Axiome bilden aber nicht die einzige Möglichkeit, (H4) und (H6) zu ersetzen. Bezüglich des Unterordnungskalküls sind z.B. die Regeln
![]() und
und
![]()
oder auch die Regeln
![]() ,
,
![]() ,
,
![]() und
und
![]()
mit den Axiomen A5 äquivalent.
Der bisher eingeführten begriffslogischen Axiomatik fehlen die partikulären
Beziehungen, d.h. die Negationen der universellen Beziehungen. Die Negation der
Art-Gattungsbeziehung entspricht dem klassischen aristotelischen o-Urteil, daß
i-Urteil kann geschrieben werden als
![]() bzw.
bzw.
![]() .
Zur Darstellung der klassischen Begriffslogik ist also mehr
notwendig als die pure Art-Gattungsbeziehung.
.
Zur Darstellung der klassischen Begriffslogik ist also mehr
notwendig als die pure Art-Gattungsbeziehung.
Auch mit den Venn-Diagrammen kann man die negierte Unterordnung beherrschen, d.h. es besteht in dieser Hinsicht durchaus Handlungsbedarf für die bisherige begriffslogische Axiomatik. Eine Möglichkeit wäre, das Axiomensystem um Regeln für die Negation der Unterordnung zu erweitern. Die entsprechenden Regeln würden nach dem Verfahren der sogenannten ,,inkonsistenten Triade``, bzw. der Kontraposition entwickelt werden, welches einer zweimaligen Anwendung der Peirce-Regel entspricht. Dabei wird die negierte Konklusion zur Prämisse und eine der Prämissen wird negiert zur Konklusion. Eine Anwendung auf die Grundregeln A6 bis A10 ergibt
-A6-
![]()
-A6-
![]()
-A7-
![]()
-A7-
![]()
-A8-
![]()
-A8-
![]()
-A9-
![]()
-A9-
![]()
-A10-
![]()
-A10-
![]()
und erzeugt einen Kalkül, den wir BV
![]() oder BL
oder BL
![]() nennen wollen, je nach Interpretation der formalen Sprache.
nennen wollen, je nach Interpretation der formalen Sprache.
Die Gültigkeit dieser Regeln in Venn-Diagrammen kann man einfach beweisen, indem man die Prämissen in die Diagramme einträgt, und dann feststellt, daß die Konklusionen jeweils folgen.
Es gibt jedoch noch eine andere Möglichkeit, die negierten Unterordnungen zu
erhalten. Diese Möglichkeit wird repräsentiert durch zwei spezielle Regeln,
die Deduktions- A11 und die Abtrennungsregel A12 in jeweils zweifacher
Ausfertigung. Diese Regeln stellen eine Verbindung zwischen der Unterordnung
,,![]() `` und der Ableitbarkeit ,,
`` und der Ableitbarkeit ,,![]() `` her:
`` her:
| A11 |
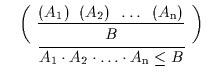 |
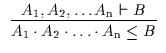 |
| A12 |
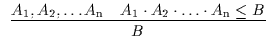 |
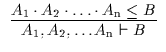
|
Die Axiome A11 und A12 definieren, ähnlich wie bei der Einführung in die Verbandstheorie, einen Hintergrundkalkül, in den die Begriffslogik eingebettet ist. Diese Axiome können aber nun so interpretiert werden, daß es sich bei dem Hintergrundkalkül wieder um den Vordergrundkalkül selbst handelt. Die zusätzlichen Axiome können wie folgt gelesen werden:
Beweis:
![\begin{displaymath}
% latex2html id marker 5093\infer
[A12]
{\overline{b} \v...
...{b} \leq 0}
{\infer
[A11]
{a \leq b}
{a \vdash b}
}
}
}
\end{displaymath}](img585.gif)
Beweis:
![\begin{displaymath}
% latex2html id marker 5094\infer
[A12]
{a, \overline{c}...
...b}}
{\infer
[A11]
{a \cdot b \leq c}
{a, b \vdash c}
}
}
\end{displaymath}](img587.gif)
Es ist also möglich, die Kontraposition bzw. die ,,inkonsistente Triade``
nachzubilden. Eine offene Frage ist natürlich noch, ob der Kalkül BV
![]() ,
der durch Anwendung der inkonsistenten Triade nur auf die
Grundregeln entsteht, gleichmächtig ist mit dem Kalkül der um die Axiome A11
und A12 erweiterten Begriffslogik, wenn diese zusätzlichen Axiome
ausschließlich für die inkonsistente Triade bzw. Kontraposition eingesetzt
werden. Die eine Richtung ist bereits erledigt, denn die Axiome -A6- bis -A10-
wurden ja durch Anwendung der inkonsistenten Triade erzeugt. Die andere Richtung
ist ungleich schwieriger und wird hier lediglich durch ein
Konstruktionsverfahren plausibel gemacht. Gegeben ist also ein Beweis mit
ausschließlich unnegierten Beziehungen, sowie eine durch Kontraposition
erzeugte Variante mit negierten Beziehungen. Der ursprüngliche Beweis wird
zunächst soweit erweitert, bis nur noch Grundregeln angewendet werden, d.h. alle Hilfssatzanwendungen werden aufgelöst. Der Beweisast, der sich an die
unnegiert gebliebene Prämisse oder Prämissen anschließt (falls vorhanden),
bleibt unverändert. Für die anderen einzelnen Beweisschritte werden jeweils
die entsprechenden kontraponierten Grundregelanwendungen eingesetzt, wobei es
gelegentlich zwei Varianten geben kann. Anschließend werden die
Beweisschritte in umgekehrter Reihenfolge angeordnet, und jeweils die passende
Variante herausgesucht. So ergibt sich ein nur auf den Axiomen des Kalküls
BV
,
der durch Anwendung der inkonsistenten Triade nur auf die
Grundregeln entsteht, gleichmächtig ist mit dem Kalkül der um die Axiome A11
und A12 erweiterten Begriffslogik, wenn diese zusätzlichen Axiome
ausschließlich für die inkonsistente Triade bzw. Kontraposition eingesetzt
werden. Die eine Richtung ist bereits erledigt, denn die Axiome -A6- bis -A10-
wurden ja durch Anwendung der inkonsistenten Triade erzeugt. Die andere Richtung
ist ungleich schwieriger und wird hier lediglich durch ein
Konstruktionsverfahren plausibel gemacht. Gegeben ist also ein Beweis mit
ausschließlich unnegierten Beziehungen, sowie eine durch Kontraposition
erzeugte Variante mit negierten Beziehungen. Der ursprüngliche Beweis wird
zunächst soweit erweitert, bis nur noch Grundregeln angewendet werden, d.h. alle Hilfssatzanwendungen werden aufgelöst. Der Beweisast, der sich an die
unnegiert gebliebene Prämisse oder Prämissen anschließt (falls vorhanden),
bleibt unverändert. Für die anderen einzelnen Beweisschritte werden jeweils
die entsprechenden kontraponierten Grundregelanwendungen eingesetzt, wobei es
gelegentlich zwei Varianten geben kann. Anschließend werden die
Beweisschritte in umgekehrter Reihenfolge angeordnet, und jeweils die passende
Variante herausgesucht. So ergibt sich ein nur auf den Axiomen des Kalküls
BV
![]() basierender Beweis für jeden durch
Kontraposition/inkonsistente Triade mittels A11 und A12 erzeugten Beweis.
basierender Beweis für jeden durch
Kontraposition/inkonsistente Triade mittels A11 und A12 erzeugten Beweis.
Darüber hinaus bieten die Axiome A11 und A12 aber auch noch eine Reihe weiterer
Möglichkeiten, denn die Verbindung von Unterordnung und Ableitbarkeit ist noch
anderweitig nutzbar. Die Möglichkeiten dieser um die Axiome A11 und A12
erweiterten Begriffslogik (der Kalkül wird BL![]() genannt) gehen vor
allem im Bereich der Beziehungsbegriffe über den Bereich der normalen
Begriffslogik hinaus. Ansonsten ergeben sich keine Änderungen, denn die
durch die Axiome erzeugte Beziehung zwischen der Ableitbarkeitsbeziehung und
der Art-Gattungs-Beziehung zeigt ja, daß auf der höheren Ebene im Prinzip die
gleichen Axiome gelten. Die Begriffslogik einschließlich A11 und A12 ist
allerdings in bezug auf ihre Möglichkeiten ,,stärker`` als die Venn-Diagramme
einschließlich Streichen und ,,Sternen``. Zumindest teilweise simulierbar wäre
das Wirken der Regeln A11 und A12 durch die parallele Anwendung mehrerer
Venn-Diagramme auf den verschiedenen Ebenen. Die Venn-Diagramme bieten zudem
keine ordentliche Möglichkeit, ,,
genannt) gehen vor
allem im Bereich der Beziehungsbegriffe über den Bereich der normalen
Begriffslogik hinaus. Ansonsten ergeben sich keine Änderungen, denn die
durch die Axiome erzeugte Beziehung zwischen der Ableitbarkeitsbeziehung und
der Art-Gattungs-Beziehung zeigt ja, daß auf der höheren Ebene im Prinzip die
gleichen Axiome gelten. Die Begriffslogik einschließlich A11 und A12 ist
allerdings in bezug auf ihre Möglichkeiten ,,stärker`` als die Venn-Diagramme
einschließlich Streichen und ,,Sternen``. Zumindest teilweise simulierbar wäre
das Wirken der Regeln A11 und A12 durch die parallele Anwendung mehrerer
Venn-Diagramme auf den verschiedenen Ebenen. Die Venn-Diagramme bieten zudem
keine ordentliche Möglichkeit, ,,![]() `` als Verknüpfungszeichen zu
behandeln, sie entsprechen also eigentlich dem Kalkül BV
`` als Verknüpfungszeichen zu
behandeln, sie entsprechen also eigentlich dem Kalkül BV
![]() .
.