3.3 Testen von vermuteten Folgerungen

Die grundlegende Funktion, die in einem Venn-Diagramm ausgeführt werden kann, ist der Test, ob sich eine vermutete Folgerung aus den gegebenen Voraussetzungen tatsächlich folgern läßt.

Dieser Test funktioniert wie folgt: Zunächst muß die Anzahl der beteiligten Grundobjekte bestimmt, und das passende Diagramm gewählt werden. Dann werden die bekannten Voraussetzungen eingetragen. Gleichungen werden dabei in zwei Halbordnungen aufgelöst. Dann wird geprüft, ob die Voraussetzungen die vermutete Folgerung enthalten.

Für die Halbordnung: Es wird geprüft, ob alle Zellen, die für die vermutete Folgerung schraffiert sein müssten, durch die Voraussetzungen schraffiert wurden. Ist dieses der Fall, so folgt die vermutete Folgerung aus den Voraussetzungen, andernfalls folgt sie nicht.

Für die Negation der Halbordnung: Es wird geprüft, ob es mindestens eine Sternsorte aus einer der Voraussetzungen gibt, die nur in den durch die Folgerung vorgegebenen Zellen vorkommt und sonst nirgendwo außerhalb. Ist dieses der Fall, so folgt die vermutete Folgerung, andernfalls folgt sie nicht.

Die eigentlich bemerkenswerteste Eigenschaft der Venn-Diagramme ist, daß die Ergebnisse bezüglich FOLGEN bzw. NICHT-FOLGEN von vermuteten Folgerungen aus den vorgegebenen Voraussetzungen definitiv sind.

Satz 3.1  

Mit Hilfe eines Venn-Diagrammes ist das FOLGEN bzw. NICHT-FOLGEN von vermuteten Folgerungen aus gegebenen Voraussetzungen in Booleschen Verbänden definitiv zu entscheiden.

Beweis: (1) Die vermutete Folgerung ist eine Halbordnung. Wir betrachten dazu die Voraussetzungen, die unnegierte Halbordnungen sind. Jede dieser Halbordnungen liegt o.B.d.A. (DNF) in der Form $a \sqsubseteq b$ vor, wobei $a$ und $b$ beliebig verknüpfte Variablen, deren Komplemente oder die Konstanten 0 oder 1 sein können. Nach Satz 2.22 gilt dann auch $a \sqcap \overline{b} \sqsubseteq 0$, falls die Halbordnung nicht bereits in dieser Form vorliegt. Die Zellen, die von $a \sqcap \overline{b}$ betroffen sind, werden schraffiert. Dieses wird für jede der betrachteten Voraussetzungen durchgeführt. Mehrfach schraffierte Zellen werden nur einfach gezählt. Die Voraussetzungen liegen danach als eine Menge von Halbordnungen der Form $x_{1} \sqcap \ldots \sqcap x_{n} \sqsubseteq 0$ vor, wobei $n$ die Zahl der Grundobjekte ist.

Gemäß Satz 2.10 liegt dann auch die Disjunktion der einzelnen betroffenen Minterme unter 0. Wir betrachten nun die vermutete Folgerung in der gleichen Weise. Dann liegt die vermutete Folgerung ebenfalls als eine Menge von Halbordnungen der Form $x_{1} \sqcap \ldots \sqcap x_{n} \sqsubseteq 0$ vor. Ist nun die Menge der Halbordnungen der vermuteten Folgerung eine Teilmenge der Menge der Halbordnungen der Voraussetzungen, so FOLGT die vermutete Folgerung, und aus der Disjunktion der durch die Voraussetzungen betroffenen Minterme können gefahrlos alle Minterme, die nicht in der Menge der Halbordnungen der vermuteten Folgerung liegen, weggelassen werden. Ist andererseits die Menge der Halbordnungen der vermuteten Folgerung keine Teilmenge der Menge der Halbordnungen der Voraussetzungen, so kann die vermutete Folgerung NICHT FOLGEN, denn dann fehlt mindestens eine Halbordnung in der Menge der Halbordnungen der Voraussetzungen. Dann aber ist es unmöglich, mit Hilfe der Voraussetzungen, die Schraffuranforderungen der vermuteten Folgerung zu erfüllen, die vermutete Folgerung kann nicht folgen.

Die Antwort FOLGT ist definitiv, durch die Angabe eines allgemeinen Beweisverfahrens. Die Antwort FOLGT-NICHT ist definitiv durch die Reduktion auf die Minterme, denn fehlende Minterme sind durch nichts zu ersetzen, da die Minterme eindeutig die $2^{(2^n)}$ verschiedenen Booleschen Funktionen charakterisieren.

(2) Die vermutete Folgerung ist die Negation einer Halbordnung. Gibt es keine verneinte Voraussetzung, so kann die vermutete Folgerung nicht folgen. Gibt es verneinte Voraussetzungen, so muß man im allgemeinen verneinte, wie unverneinte Halbordnungen betrachten. Für jede der verneinten Halbordnungen ist die folgende Prozedur durchzuführen:

Jede der verneinten Halbordnungen kann mit Hilfe von Satz 2.33 und Satz 2.34 in die Form $( x_{1,1} \sqcap \ldots \sqcap x_{1,n}) \sqcup \ldots \sqcup ( x_{m,1} \sqcap \ldots \sqcap x_{m,n}) \not\sqsubseteq 0$ gebracht werden. Wenn einige der so betroffenen Zellen durch Halbordnungen schraffiert sind, so können diese nach Satz 2.32 aus der Disjunktion der Minterme entfernt werden. Für die übrigbleibenden Zellen jeder verneinten Voraussetzung muß geprüft werden, ob sie eine Teilmenge der Zellen der vermuteten Folgerung sind. Liegt auch nur eine Zelle der Voraussetzung nicht in der Menge der Zellen der vermuteten Folgerung, so ist die Existenz einer Zelle innerhalb der Menge der Zellen der vermuteten Folgerung nicht mehr gesichert. Die vermutete Folgerung behauptet nur, daß mindestens eine der Zellen der vermuteten Folgerung existiert, bezogen auf die verneinte Voraussetzung könnte es dann aber gerade diese außerhalb liegende Zelle sein. Gibt es mindestens eine verneinte Voraussetzung, die die Bedingungen der vermuteten Folgerung erfüllt, so folgt die vermutete Folgerung. Erfüllt keine der Voraussetzungen diese Bedingungen, so kann die vermutete Folgerung nicht folgen.

Die Antwort FOLGT ist definitiv, durch die Angabe eines allgemeinen Beweisverfahrens. Die Antwort FOLGT-NICHT ist definitiv, denn wenn erstens überhaupt keine verneinte Voraussetzung existiert, kann auch keine verneinte vermutete Folgerung zutreffen oder zweitens ein Stern einer Sternsorte noch außerhalb der vermuteten Folgerung $a \not\sqsubseteq 0$ existiert, also z.B. $a \sqcup b \not\sqsubseteq 0$ gilt, so müßte, damit die vermutete Folgerung $a \not\sqsubseteq 0$ folgt, gelten: $a \sqcup b \not\sqsubseteq 0 ~ \Rightarrow ~ a \not\sqsubseteq 0$. Kontraposition ergibt: $a \sqsubseteq 0 ~ \Rightarrow ~ a \sqcup b \sqsubseteq 0$ und das folgt, wie die Reduktion auf die Minterme zeigt, in keinem Fall.

Die hier vorgestellten Verfahren bilden die Grundlage für die Möglichkeit, rein mechanisch Beweise aus den Diagrammen zu erzeugen, oder aber genau anzugeben, was minimal noch fehlt, um dafür zu sorgen, daß die vermutete Folgerung wirklich folgt.

Ein Beispiel, in dem alle oben besprochenen Fälle vorkommen:

Es gelten die folgenden Voraussetzungen:

1.

$a \sqsubseteq b$

2.

$b \not\sqsubseteq a$

3.

$b \sqcap c \sqsubseteq d$

4.

$b \not\sqsubseteq c$

5.

$c \not\sqsubseteq b$

6.

$c \not\sqsubseteq a \sqcup b$

7.

$c \sqsubseteq a \sqcup d$

Trägt man diese Voraussetzungen in ein Venn-Diagramm ein, so ergibt sich:

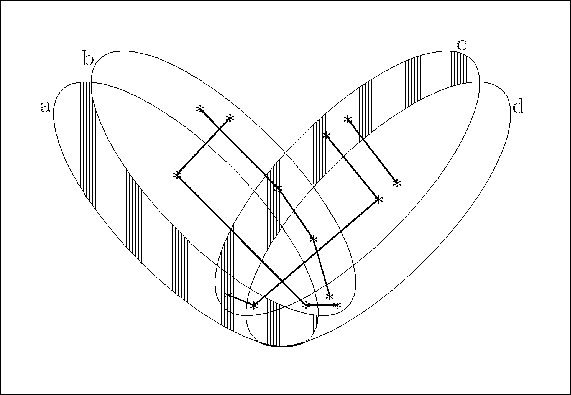
Nun kann man z.B. die folgenden Vermutungen abtesten:

1.

$c \sqsubseteq d$

2.

$d \not\sqsubseteq b$

3.

$a \sqsubseteq \overline{c}$

4.

$b \not\sqsubseteq d$

5.

$a \sqcap c \not\sqsubseteq \overline{b} \sqcup \overline{d}$

Der Test auf FOLGEN bzw. NICHT-FOLGEN ergibt dann, wobei waagerechte Schraffur Halbordnungen andeutet und eingekreiste Sterne diese als betroffen markieren:

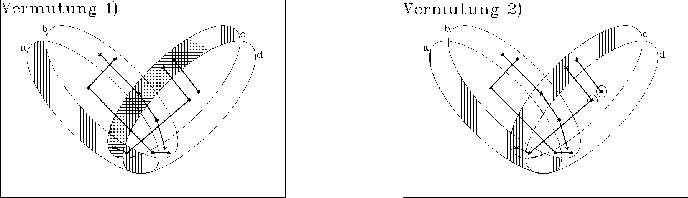
Vermutung 1) FOLGT, denn alle waagerecht schraffierten Zellen sind auch senkrecht schraffiert.

Vermutung 2) FOLGT, denn beide eingekreisten Sterne kennzeichnen jeweils eine Sternsorte, die nur in den von der Vermutung betroffenen Zellen auftritt und sonst nicht.

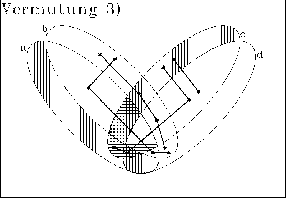
Vermutung 3) FOLGT NICHT, denn es sind nicht alle waagerecht schraffierten Zellen auch senkrecht schraffiert.

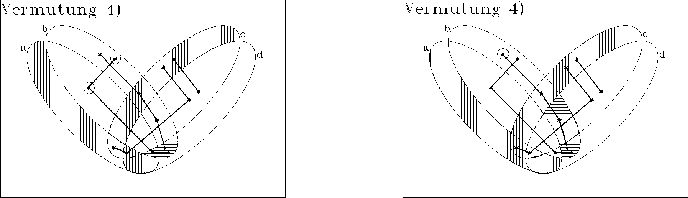
Vermutung 4) FOLGT NICHT, denn es gibt keine Sternsorte, die nicht auch außerhalb der durch die Vermutung betroffenen Zellen auftritt. Die waagerechte Schraffur gibt jeweils an, welche Zellen noch gestrichen sein müssten, damit die Vermutung folgt.

Vermutung 5) FOLGT NICHT, weil es überhaupt keinen Stern in den durch die Vermutung betroffenen Zellen gibt.

Wie man sieht, ist es ganz einfach die Voraussetzungen in ein Diagramm einzutragen. Durch dieses Eintragen, werden im Prinzip alle Axiome/Sätze der linearen Darstellung des Booleschen Verbandes angewendet. Man selbst muß keine Regeln anwenden. Das Prüfen ist sehr anschaulich, denn man muß nur den Zustand bestimmter Zellen betrachten, um zu einer definitiven Entscheidung zu kommen.