3.2 ,,Sternen`` von Zellen

Die logische Einbettung der Booleschen Verbände erlaubte die Behandlung negierter Gleichungen bzw. Halbordnungen. Die Negation der Halbordnungsbeziehung kann dagegen im Venn-Diagramm direkt behandelt werden:

$a \not\sqsubseteq b$ entspricht $a \sqcap b \not = a$, d.h. $a \sqcap \overline{b}$ existiert.

$a \not\sqsubseteq \overline{b}$ entspricht $a \sqcap \overline{b} \not = a$, d.h. $a \sqcap b$ existiert.

$\overline{a} \not\sqsubseteq b$ entspricht $\overline{a} \sqcap b \not = \overline{a}$, d.h. $\overline{a} \sqcap \overline{b}$ existiert.

$\overline{a} \not\sqsubseteq \overline{b}$ entspricht $\overline{a} \sqcap \overline{b} \not = \overline{a}$, d.h. $\overline{a} \sqcap b$ existiert.

Das Existieren einer Zelle wird dadurch repräsentiert, daß die entsprechende Zelle mit einem Stern versehen wird. Dann sehen die vier verschiedenen negierten Halbordnungsvarianten wie folgt aus:

Ein Ausdruck kann auch wieder dazu führen, daß mehrere Zellen ,,gesternt`` werden müssen. Um diese Sterne von den Sternen eventuell vorhandener anderer Ausdrücke zu unterscheiden, sind diese durch einen spannenden Graphen miteinander zu verbinden. Gilt z.B. $a \sqcup ( b \sqcap c ) \not\sqsubseteq 0$, so wird dieses wie folgt im Venn-Diagramm dargestellt:

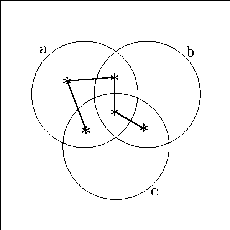
Was bedeuten nun die durch die Striche verbundenen Sterne? Sie bedeuten, daß mindestens eine der gekennzeichneten Zellen existieren muß, nicht etwa alle. Das ist so, weil es sich um eine Verneinung der Halbordnung handelt. Das Schraffieren mehrerer Zellen durch eine Halbordnungsbeziehung bedeutet, daß alle gekennzeichneten Zellen nicht existieren. Negiert man einen solchen Ausdruck, so erhält man einen Ausdruck, der besagt, daß die erste Zelle existiert oder die zweite Zelle existiert oder ... oder die $n$-te Zelle existiert.

Die Schraffur einer gesternten Zelle löscht diesen Stern. Diese Löschung kann bedenkenlos vorgenommen werden solange immer noch ein unschraffierter Stern des jeweiligen spannenden Graphen existiert. Sind alle Sterne eines spannenden Graphen schraffiert, so liegt ein Widerspruch in den Voraussetzungen vor.

Die Einführung der Sternungsoperation bewirkt eine echte Verstärkung der Möglichkeiten der Venn-Diagramme gegenüber den normalen ,,Booleschen`` Fähigkeiten.