3.1 Streichen von Zellen

Es ist üblich, die nicht existierenden Zellen im Diagramm zu streichen, zu schraffieren. Dann sehen die vier verschiedenen Halbordnungsvarianten wie folgt aus:

Von einer Streichung können auch mehrere Zellen betroffen sein. Es gelte z.B. $a \sqsubseteq b$ und $b \sqsubseteq c$. Aus diesen Vorgaben ist insbesondere $a \sqsubseteq c$ ablesbar.

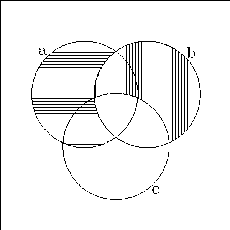
So nebenbei ist damit auch (H3), eines der Axiome der Halbordnungsstrukturdefinition bewiesen. Gilt $a \sqsubseteq b$ und $b \sqsubseteq a$, so existieren die Zellen $a \sqcap \overline{b}$ und $\overline{a} \sqcap b$ nicht, sind also schraffiert, somit existiert nichts von $a$ außerhalb von $b$ und nichts von $b$ außerhalb von $a$. Es ist also $a = b$.

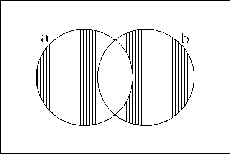
Daher ist (H2) bewiesen. Der Schnitt von $a$ mit $a$ ergibt wiederum $a$, es gilt daher gemäß Übersetzung $a \sqcap a = a$. Nach Definition ist das gleichbedeutend mit $a \sqsubseteq a$ (H1). Der Schnitt von $a$ mit $a$ läßt sich kaum richtig im Venn-Diagramm darstellen, würde er doch verlangen, zwei verschiedene Regionen im Diagramm zu haben, die $a$ repräsentieren sollen, was aber die Definition nicht erlaubt.

In Satz 2.38 war zu sehen, daß die beiden Seiten der beiden Distributivgesetze die gleichen Zellen im Venn-Diagramm betreffen. Betrachtet man nun die in (H4) aufgeführten Halbordnungen, so müssen durch diese keine Zellen gestrichen werden, denn keine Zelle ist links und nicht rechts.