Das Venn-Programm

Die Venn-Diagramme sind eine Technik zur Darstellung logischer Zusammenhänge, die 1880 von John Venn (1834-1923) eingeführt wurde.

Ein Venn-Diagramm besteht aus einem "Rahmen", der das "Universum" darstellt, und darin ein beliebiges geschlossenes Gebilde (z.B. ein Kreis) für jedes auftretende Objekt. Es erübrigt sich, zu einem Objekt auch sein Negat (sein Gegenteil) einzuführen, denn letzteres ist nichts anderes als das "Äußere" des jeweiligen "Kreises". Da die "Kreise" darüber hinaus so angeordnet werden, daß sich alle denkbaren Schnittflächen ergeben (hier für n=1 bis 5), entfällt auch das Einführen von verknüpften Objekten, die durch "und" und "oder" aus vorhandenen Grundobjekten gebildet werden.

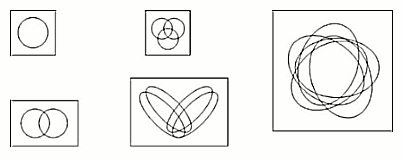
Vorteilhaft ist, daß in die Venn-Diagramme die Axiomatik der Booleschen Verbände, und damit der Begriffslogik, gleichsam eingearbeitet ist. Es genügt, die Prämissen (das Wissen) nach einem mechanischen Verfahren in ein Diagramm einzutragen. Dann kann man sofort mechanisch prüfen, ob mögliche Konklusionen (Vermutungen) aus den Prämissen FOLGEN oder NICHT FOLGEN. Es brauchen keine Regeln angewendet zu werden, um Konklusionen zu testen, man kann nicht mit einem Beweisansatz in die Irre laufen, und vor allem sind die Ergebnisse definitiv. Vor allem bieten die Diagramme daher auch didaktische Vorteile.

Naturgemäß hat diese Diagrammtechnik Grenzen. Bei mehr als vier oder fünf Grundobjekten wird das Eintragen der Prämissen unhandlich und das Überprüfen der Konklusionen schwierig. Die oben erwähnten mechanischen Verfahren machen die Diagrammtechnik allerdings für den Einsatz auf Computern interessant. Dabei kann es nicht sinnvoll sein, die Grafik zu übernehmen, vielmehr sollte lediglich die Struktur der Diagramme auf den Computer übertragen werden (hier für 1 bis 3 Dimensionen).

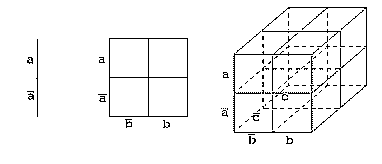
Die Übertragung auf den Rechner bietet auch noch weitere Vorteile. So ergibt sich die Möglichkeit, noch weitere Operationen einzuführen, die an den Diagrammen vorgenommen werden können.

• das Bestimmen der (Venn-)minimal noch fehlenden Prämissen, wenn eine Konklusion nicht folgt
• das mechanische Konstruieren von Beweisen, wie man von den Prämissen zur Konklusion kommt, wenn diese aus den Prämissen folgt
• die Angabe eines Überblickes, was alles aus den Prämissen folgt

Die Beschäftigung mit dieser vermeintlich veralteten, unzeitgemäßen Repräsentation Boolescher Verbände erweist sich unter dem Blickwinkel der Computerunterstützung als ein interessantes Instrument, die Vor- und Nachteile der heute üblichen linearen Darstellung Boolescher Verbände zu beleuchten.

Genauere theoretische Angaben finden sich hier.

Das Venn-Programm liegt in einer Pascal-Version (DOS) 114 kB sowohl deutsch als auch in einer englischen Version, sowie in einer relativ portablen C++-Version (DOS, OS/2) 323 kB, sowie für Linux (glibc2, 133 kB) vor.