Andreas Otte
08.11.1987
Dieser Text versteht sich als Erweiterung von ``Neues System der Logik'' und verwendet dessen Regelstruktur und -bezeichnungen.
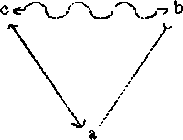
Die Regel 1.1 legt es nahe, jede Identität durch eine Disparität und eine Diversität auszudrücken. Man könnte dann ganz auf die unsymmetrische Identitätsbeziehung verzichten und einen Kalkül nur aus symmetrischen Beziehungen aufbauen (Regel 1.1:).
Um die Identitätsbeziehung zwischen a und b darstellen zu können, bräuchte
man also noch einen dritten Begriff c, der zunächst einmal völlig
unbestimmt ist. Es gibt allerdings zwei Begriffe, die ausgezeichnet sind;
die beiden Negatbegriffe. In der Wahl sind wir beliebig, wir wählen
.
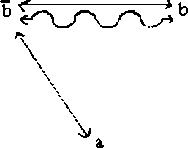
Wobei wir allerdings nur die Disparität in der Negatbeziehung zwischen b
und
benötigen. Die Identitätsbeziehung zwischen a und b wird
also durch die Diversität zwischen a und
dargestellt, die
Disparität zwischen b und
ist trivial.
Welche Grundregeln gibt es?
Betrachten wir dazu die Regel 1.2a, das alte ''dictum de nullo'':
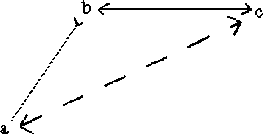
Die Begriffslage ohne Identität müßte so aussehen:
Verallgemeinert zu einer Grundregel ergibt sich Regel S.1a:
Die duale Regel S.1b ist dann:
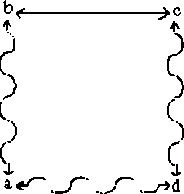
Diese Regel ist anwendbar auf die Begriffslage der Regel 1.2b. Die Regel 1.3 würde dann so aussehen:
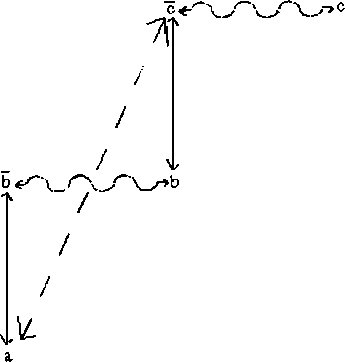
Die gestrichelte Diversität müßte gefolgert werden, damit nach 1.1 a Art von c ist. Das ergibt sich aber ganz einfach aus der Regel S.1a.
Man braucht also nur zwei Regeln für die unverneinten Beziehungen. Die Regel 1.1 gibt es nicht mehr, sie ist sozusagen zur ''"Ubersetzungsregel'' in den übergeordneten Kalkül geworden, in dem es die Identität gibt. Vielmehr ist Regel 1.1 nunmehr eine Art ''Grundformel'', die etwas über die Beziehung zweier Begriffe unter Verwendung eines dritten aussagen. Die Regeln 1.2a und 1.3 werden durch S.1a und 1.2b wird durch S.1b abgedeckt.
Nun zu den Regeln mit unverneinten Beziehungen. Durch die ''inconsistente Triade'' ergibt sich:
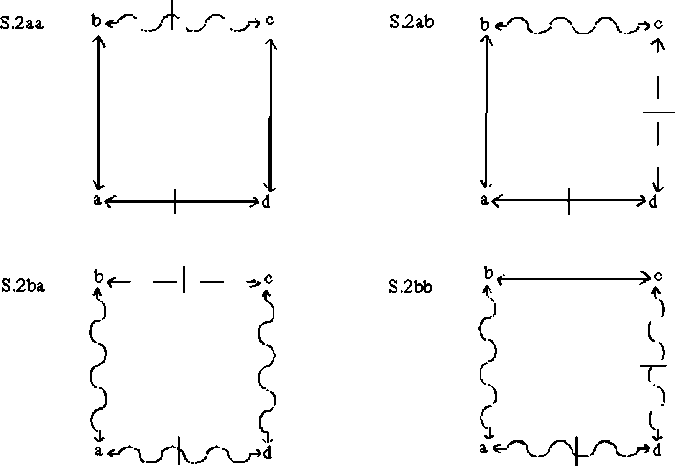
Wie werden nun die verneinten Identitätsbeziehungen dargestellt?
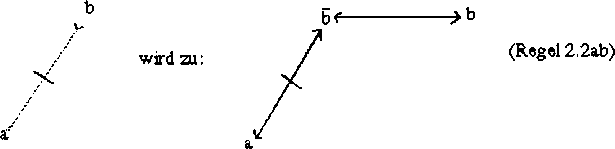
und
Nun zu den Syllogismen:
Numerieren wir zunächst die jetzt nur noch zur Verfügung stehenden Urteile:
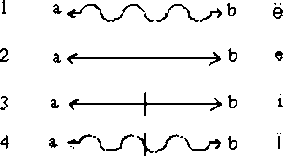
Dann ergeben sich die folgenden Kombinationsmöglichkeiten:
|
|
In den anderen Fällen läßt sich nichts folgern, manchmal handelt es sich um ''Grundformeln (G)'', also Begriffslagen, die Identitäts- oder verneinte Identitätsbeziehungen ausdrücken, ohne daß wir dafür ein eigenes Zeichen haben.
Die Syllogistik, also die Lehre von den Beziehungen zwischen drei Begriffen, scheint nicht mehr durchführbar. Nimmt man aber noch die Negatbegriffe mit hinzu, so entfaltet sie sich wieder. Denn dann kann man die Identitätsbeziehungen wieder darstellen. Betrachten wir dazu die alte Nummerierung:
| Nummer | Darstellung mit Identität | Darstellung ohne Identität |
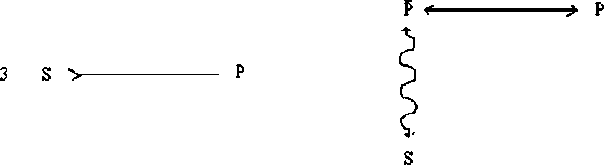
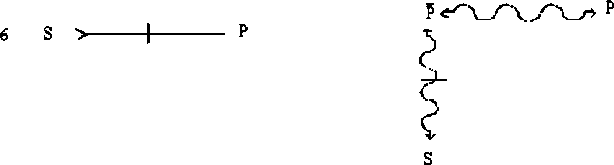
Die Urteile 3 - 6 könnte man als zusammengesetzte Urteile bezeichen.
Betrachten wir zunächst die Schlüsse nach dem ''Dictum de ommni et nullo''. Dann sind:
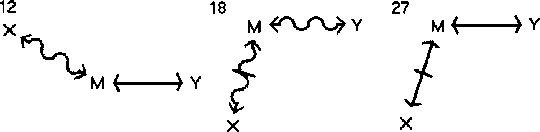
Grundformeln.
Dann schließt (wobei M der Mittelbegriff ist und X und Y die beiden Begriffe, über deren Beziehung etwas ausgesagt werden soll. Freie Stellen sind durch beliebige Begriffe zu besetzen, die die geforderten Bedingungen erfüllen, vorzugsweise also durch die Negatbegriffe von X und Y.):
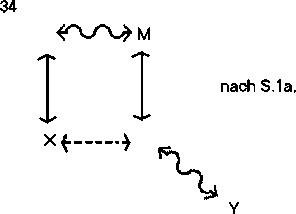
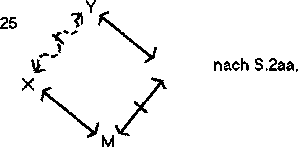
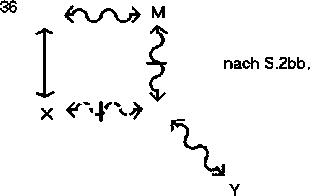
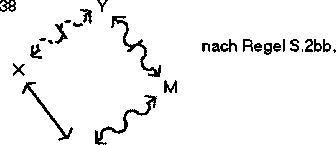
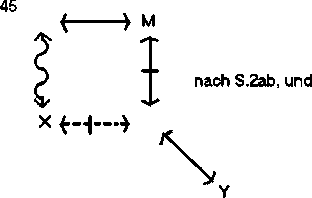
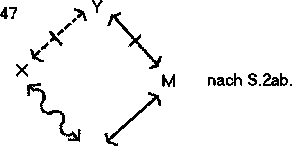
Die Schlüsse nach dem Vergeßbarkeitsprinzip:
M ist widerspruchsfrei wird dargestellt durch:
M ist nicht inhaltsleer wird dargestellt durch:
Dann schließt:
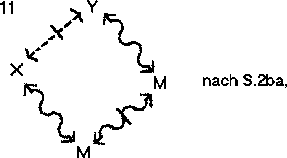
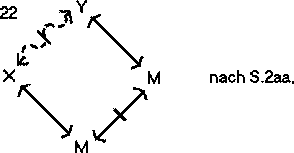
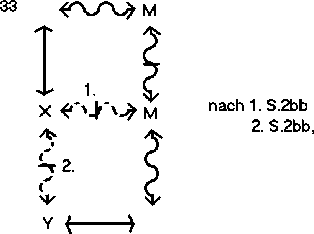
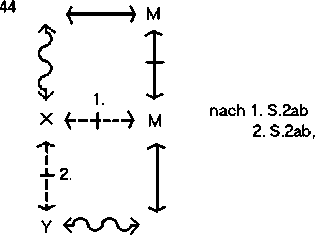
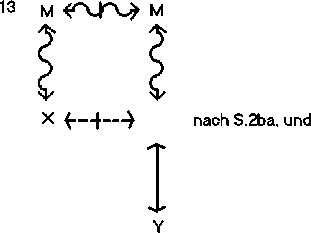
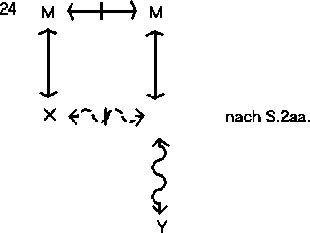
Die gesamte Syllogistik ist mit den sechs S-Regeln darstellbar.
Wir können also mit diesen Axiomen prinzipiell alles erreichen, was wir auch mit den alten Regeln schon konnten, wenigstens im Bereich der Syllogistik. Es gibt keinen Grund, warum das bei den Definitionen nicht so sein sollte. Die Begriffslagen werden allerdings durch die notwendige Einführung von zusätzlichen Begriffen sehr kompliziert und wenig übersichtlich.
